Hybridation de méthodes

complètes et incomplètes pour la

résolution de CSP

Thèse de doctorat

Spécialité : Informatique

École Doctorale STIM

Sciences et Technologies de l’Information et des Matériaux
Présentée et soutenue publiquement

Le	27 Octobre 2006
À	Nantes
Par	Tony LAMBERT

Devant le jury ci-dessous :

Président :	Jin-Kao Hao,	Professeur à l’Université d’Angers
Rapporteurs :	François Fages	Directeur de Recherche, INRIA Rocquencourt
	Bertrand Neveu,	Ingénieur en Chef des Ponts et Chaussées, HDR
Examinateurs :	Steve Prestwich,	Maître-assistant à l’Université de Cork
Directeurs de thèse :	Éric Monfroy,	Professeur à l’Université de Nantes
	Frédéric Saubion,	Professeur à l’Université d’Angers

Sommaire

Contexte de travail

La famille des problèmes de satisfaction de contraintes [ Tsang1993, Waltz1975] (Constraint Satisfaction Problems CSP) couvre un grand nombre de problèmes pratiques (planification, ordonnancement, emploi du temps ...) dont de nombreux exemples ont été recensés et catalogués depuis plusieurs décennies (le lecteur pourra consulter, en autres, la CSPLib [ Gent et al. ]). D’un point de vue calculatoire, les problèmes considérés induisent bien souvent des complexités algorithmiques élevées puisque bon nombre d’entre eux relèvent de la classe des problèmes NP-complets [ Garey and Johnson1978, Papadimitriou1994]. Ces problèmes partagent une structure de description commune, basée sur un formalisme très simple, qui autorise une modélisation claire et intuitive.

Plus précisément, étant donné un ensemble de n variables X={x₁,...,x_n} dont les domaines de valeurs respectifs sont dans l’ensemble D={D₁,...,D_n} (nous considérons dans cette thèse des domaines discrets), une contrainte quelconque est une relation c ⊆ D₁×...×D_n. Un CSP est alors classiquement défini par un triplet (X,D,C) où C est l’ensemble des contraintes. Une solution correspond à une affectation de valeurs aux variables qui satisfait les contraintes et les restrictions imposées par les domaines. On distingue alors les problèmes satisfiables, possédant au moins une solution, et les problèmes insatisfiables.

En terme de résolution opérationnelle, plusieurs voies peuvent être envisagées selon que l’on s’intéresse à décider de l’existence d’une solution, à son calcul effectif ou encore au calcul exhaustif de l’ensemble des solutions.

Au cours des vingt dernières années, de nombreux algorithmes et systèmes ont été développés pour résoudre les CSP. Classiquement, on identifie deux grandes familles au sein de ces techniques de résolution. D’une part, les méthodes complètes (ou exactes), dont l’objectif est de répondre au problème de décision et donc de prouver la satisfiabilité d’un problème, ou son insatisfiabilité le cas échéant. En général, ces méthodes permettent également d’extraire l’ensemble des solutions d’un problème. D’autre part, les méthodes incomplètes (ou approchées) abordent généralement la résolution d’un CSP comme un problème d’optimisation combinatoire pour lequel il s’agit de calculer une affectation satisfaisant le plus grand nombre de contraintes, l’objectif final étant de les satisfaire toutes. Dans ce cas, on parle aussi de problème de satisfiabilité maximale (MaxCSP) ¹. Contrairement aux approches complètes, les méthodes incomplètes ne peuvent pas conclure à l’insatisfiabilité d’un problème.

Du point de vue des techniques utilisées, les approches complètes reposent principalement sur une recherche arborescente incluant des notions de consistance locale des contraintes [ Mackworth1992, Mohr and Henderson1986]. Un arbre de recherche permet la construction incrémentale d’affectations, attribuant, à chaque noeud, des valeurs aux variables et testant progressivement la validité des choix effectués vis-à-vis des contraintes. Afin de réduire l’espace de recherche, on utilise généralement la structure et les propriétés de ces contraintes pour élaguer l’arbre ainsi que diverses stratégies de construction et de parcours.

Ces techniques sont à la base des systèmes de programmation par contraintes (on pourra se reporter par exemple à [ van Hentenryck1989, Fages1996, Mariott and Stuckey1998, Fruewirth and Abdennadher2003, Dechter2003] pour plus de précisions) concrétisés par de nombreux langages et solveurs (Prolog IV [ Colmerauer1994], Chip [ Aggoun and Beldiceanu1991], Ilog Solver [ ILOG2000], CHOCO [ Laburthe2000]...). Rappelons que la programmation par contraintes a connu ses premiers succès au travers de la programmation logique avec contraintes, paradigme au sein duquel la programmation logique sert de langage hôte pour la formulation du problème et des contraintes [ Jaffar and Lassez1987, Fages1996, Colmerauer1990].

Les approches incomplètes reposent, quant à elles, essentiellement sur l’utilisation d’heuristiques [ Aarts and Lenstra1997, Hao et al. 1999] et particulièrement d’algorithmes basés sur la recherche locale. L’objectif de ces approches est d’explorer l’espace de recherche (dans le cas des CSP, l’ensemble des affectations possible) au moyen d’heuristiques plus ou moins sophistiquées et ce, afin d’en extraire au plus vite une solution. Deux grandes notions sont alors mises en oeuvre. D’un côté, l’intensification consiste à fouiller une zone précise de l’espace afin d’en extraire un optimum local ou mieux, une solution. D’un autre côté, la diversification a pour but de déplacer la recherche dans des zones variées de l’espace. L’efficacité d’une méthode incomplète réside alors dans l’alternance de ces deux phases, gérées au moyen de diverses structures et stratégies, ce qui a donné naissance à la famille des méthodes dites métaheuristiques. Au sein de cette famille, nous distinguerons deux grandes classes qui seront utilisées dans le cadre de nos travaux.

D’un côté, les méthodes de recherche locale explorent l’espace de recherche de proche en proche, se déplaçant d’une affectation vers une affectation voisine, guidées par une fonction évaluation (correspondant, par exemple, au nombre de contraintes violées). Divers algorithmes ont alors été proposés [ Kirkpatrick et al. 1983, Glover and Laguna1997, Aarts and Lenstra1997], introduisant des techniques de contrôle afin de garantir un équilibre entre diversification et intensification et une efficacité globale de résolution. Afin de faciliter la conception et l’utilisation de tels algorithmes pour les CSP, on dispose également de bibliothèques spécialisées, telles que EasyLocal++ [ Gaspero and Schaerf2003] mais également de langages dédiés tels que Localizer [ Michel and Hentenryck1997] ou plus récemment Comet [ van Hentenryck and Michel2005].

D’un autre côté, nous trouvons la classe des algorithmes évolutionnistes [ Holland1975b, Goldberg1989b, Michalewicz1996] qui gèrent un ensemble de configurations d’un problème et les font évoluer dans le but d’atteindre une solution. Les mécanismes opérationnels s’inspirent du principe de l’évolution naturelle et, au-delà de cette métaphore, ces méthodes se sont avérées très utiles pour la résolution de problèmes combinatoires complexes (conférences GECCO, PPSN, CEC et EvoCOP).

Lorsqu’il s’intéresse à l’utilisation effective de toutes ces méthodes, l’utilisateur se trouve confronté à un dilemme. En effet, si les méthodes complètes présentent davantage de garanties en terme de résultats (preuve d’insatisfiabilité, obtention possible de l’ensemble des solutions), elles trouvent toutefois leurs limites avec l’augmentation de la taille et de la complexité des problèmes considérés. En effet, en particulier dans le cas de problèmes NP-complets, l’explosion combinatoire de l’espace de recherche induit un coût de calcul prohibitif. Dans cas, mais au détriment de la complétude de la résolution, l’utilisateur peut alors se tourner vers les méthodes incomplètes qui ont prouvé leur efficacité en terme de passage à l’échelle.

Dans ce contexte, de nouveaux langages et systèmes, tels que le langage Salsa [ Laburthe and Caseau2002], permettent à l’utilisateur de spécifier des algorithmes de recherche globale ou locale, ou encore des algorithmes hybrides.

Un très grand nombre de travaux ont été menés sur l’hybridation entre des approches complètes et des méthodes métaheuristiques, en particulier entre programmation par contraintes et recherche locale (citons par exemple [ Jussien and Lhomme2002, Prestwich2000, Pesant and Gendreau1996, Shaw1998]). On pourra se reporter à [ Focacci et al. 2002] pour un panorama plus général. Ces algorithmes, hybridant recherche locale et techniques d’exploration complètes, correspondent souvent à des réponses spécifiques dédiées à des problèmes particuliers. On peut distinguer deux grands types de combinaison au sein de ces algorithmes selon que :

- la recherche locale vise à améliorer un algorithme complet : à certains n uds de l’arbre de recherche construit par la méthode complète, une recherche locale est utilisée afin d’atteindre une solution à partir d’une affectation partielle ou bien encore afin d’améliorer une affectation donnée. La recherche locale peut également être envisagée comme outil de réparation.

ou, inversement que

- les méthodes complètes servent à guider la recherche locale : la propagation de contraintes est utilisée pour réduire le voisinage d’un point ou l’espace de recherche dans sa totalité. Les techniques complètes peuvent aussi servir à explorer le voisinage d’un point pour déterminer le prochain mouvement à effectuer lors du processus de recherche locale.

Notons que d’autres travaux combinent par ailleurs algorithmes évolutionnaires et programmation par contraintes [ Madeline2002, Riff Rojas1996, Tam and Stuckey1999].

Ces approches, si différentes qu’elles soient, partagent souvent une même philosophie dans leur conception : un mécanisme est considéré comme le processus maître de la recherche et les autres techniques viennent à son aide comme autant d’heuristiques améliorant ses performances. De ce fait, un tel schéma général rend difficile une réelle coopération entre les différentes approches. Toutefois, les résultats obtenus par les approches hybrides nous poussent de plus en plus à nous tourner vers ce type de démarche pour concevoir des solveurs de plus en plus efficaces, tirant profit de avantages respectifs des méthodes combinées.

Motivations et contributions

Finalement, l’ensemble des techniques que nous venons de décrire est vaste, leurs principes fondamentaux de résolution sont très variés et leurs propriétés diverses. De plus, ces méthodes sont formulées de manières très hétérogènes : algorithmes dédiés, stratégies, propriétés, systèmes plus ou moins génériques ... Il peut donc s’avérer complexe de comprendre précisément leur fonctionnement et d’identifier leurs propriétés afin de bénéficier au mieux de leurs atouts. La nécessité de disposer d’un cadre formel, permettant de décrire et de caractériser les processus opérationnels de ces techniques, se faisait donc réellement sentir.

Dans le contexte de la résolution des CSP par des solveurs complets, K. Apt a proposé une formalisation des opérations de réduction des domaines des variables au moyen des propriétés de consistance locale en terme de calcul de point fixe d’un ensemble de fonctions sur une structure ordonnée [ Apt1997, Apt1999, Apt2003]. Dans ce modèle, on itère un ensemble d’opérateurs qui abstraient la structure des contraintes. Ce cadre formel permet de mettre en avant les propriétés principales de ces mécanismes de résolution (convergence et terminaison).

Dès lors, en nous basant sur ces travaux, nous avons décidé de les étendre pour prendre en compte un ensemble plus large de techniques de résolution et, en particulier, les méthodes incomplètes. L’objectif d’un tel travail est de permettre une intégration plus homogène de ces paradigmes de résolution afin d’en faciliter la combinaison dans le cadre d’algorithmes de résolution hybrides.

Nous avons donc proposé un nouveau cadre basé sur la notion d’itérations chaotiques de fonctions sur un ordre partiel, étendant ainsi les travaux de K. Apt. Ce cadre permet de modéliser de manière uniforme la résolution des CSP par des méthodes complètes (filtrage des domaines des variables, propagation de contraintes et découpe des domaines) et par des méthodes incomplètes (recherche locale et algorithmes génétiques). Nous pouvons alors abstraire les structures et les mécanismes effectifs de la résolution, autorisant ainsi des combinaisons plus homogènes entre les processus. Nous sommes également en mesure de caractériser plus clairement le déroulement et les résultats des processus de résolution hybrides et définir leurs principales propriétés. Enfin, ce cadre peut servir de base au prototypage et à la définition de nouvelles stratégies de résolution et de coopération entre les méthodes.

Afin de mettre en avant les atouts de ce nouveau formalisme, nous avons développé un système qui intègre les principaux composants que nous avons définis de manière formelle et permet, au travers d’un algorithme générique, de simuler des stratégies de résolution hybrides variées. Nous présenterons donc un certain nombre de résultats expérimentaux obtenus sur divers jeux d’essai, qui permettent de souligner les atouts et avantages d’une résolution hybride des CSP.

Le document s’articule de la manière suivante.

Organisation de la thèse

Le manuscrit se décompose en deux parties. La première présente l’état de l’art des méthodes de résolution de CSP. Nous rappelons tout d’abord les notations et les principales caractéristiques d’une modélisation en CSP ainsi que des exemples. Ensuite, la résolution par des méthodes complètes est décrite, introduisant les notions de consistances, de filtrage, de propagation et les algorithmes en faisant usage. Puis, nous présentons la résolution par les méthodes incomplètes, de la recherche locale aux algorithmes génétiques. Après un survol des hybridations existantes entre ces méthodes par collaboration ou intégration, nous présentons le cadre formel proposé par K. Apt pour une modélisation de la propagation de contraintes sur une structure ordonnée.

La seconde partie est consacrée à l’extension des travaux de K. Apt pour l’hybridation des méthodes complètes et incomplètes. Nous introduisons tout d’abord la notion d’échantillon qui nous permet par la suite une intégration de la recherche locale au sein d’un modèle hybride. Ce modèle est alors mis en uvre dans diverses expérimentations. Ensuite, nous proposons un cadre pour l’hybridation des algorithmes génétiques et des méthodes complètes pour une application à des problèmes d’optimisation sous contraintes. Enfin, dans un dernier chapitre, nous présentons un cadre général et uniforme des notions vues précédemment avant une conclusion générale qui résumera nos contributions et ouvrira sur des différentes perceptives de recherches.

Part 1

Méthodes de résolution des

problèmes de satisfaction

de contraintes

Chapitre 1

Les problèmes de satisfaction

de contraintes

Dans ce chapitre, nous présenterons les principales notions liées aux problèmes de satisfaction de contraintes (Constraint Satisfaction Problem CSP) qui sont au c ur de cette thèse. Des exemples de problèmes sous forme CSP illustrent le formalisme.

1.1 Introduction

Beaucoup de problèmes issus de l’Intelligence Artificielle (IA) ainsi que d’autres branches de l’informatique peuvent être modélisés comme des problèmes de satisfaction de contraintes (CSP) [ Nadel1990]. Nous trouvons des exemples en conception de scènes en 3D [ Chakravarthy1979, Davis and Rosenfeld1981], en maintien de la cohérence [ Dechter1987, Dechter and Dechter1988, Croker and Dhar1993], en ordonnancement [ Dhar and Ranganathan1990, Fox1987, Fox et al. 1989, Petrie et al. 1989, Prosser1989, Rit1986], en raisonnement temporel [ Allen1983, Allen1984, Dechter et al. 1991, Vilain and Kautz1986, Tsang1987], en théorie des graphes [ McGregor1979, Bruynooghe1985], en architecture [ Eastman1972], en planification d’expérimentations génétiques [ Stefik1981], en conception de circuit [ de Kleer and Syssman1980], en conception et fabrication de machines [ Frayman and Mittal1987, Navinchandra1991], ou encore en raisonnement diagnostique [ Geffner and Pearl1987]. La modélisation d’un problème sous forme de CSP se révèle souvent souvent pratique et intuitive.

Dans ce qui suit nous rappellerons les notations, les définitions liées à ce formalisme ainsi que des exemples de son utilisation.

1.2 Le modèle CSP et ses principales caractéristiques

Un problème de satisfaction de contraintes (CSP) est généralement présenté sous la forme d’un ensemble de variables, auxquelles sont associés des domaines, ainsi qu’un ensemble de contraintes.

Chaque contrainte est définie sur un sous-ensemble de l’ensemble des variables et limite les combinaisons de valeurs que peuvent prendre ces variables. La résolution d’un CSP consiste à trouver une affectation de valeur pour chaque variable de telle sorte que l’ensemble des contraintes soit satisfait. Pour certains problèmes, le but est de trouver toutes ces affectations.

Nous allons par la suite présenter non pas le cadre général, mais nous restreindre à des domaines finis de valeurs discrètes. Cette limitation se traduit dans les exemples présentés et, nous verrons par la suite, se justifie par des expérimentations pour des problèmes à domaines finis.

Définition 1 [Problème de satisfaction de contraintes] Un problème de satisfaction de contraintes (CSP) [ Tsang1993] est défini par un triplet (X,D,C) où:

X = { x₁,..., x_n} est l’ensemble fini des n variables du problème,

D = {D_x₁,...,D_{x_n}} est l’ensemble des n domaines finis pour les variables. D_{x_i} est l’ensemble des valeurs possibles pour la variable x_i,

C = {c₁,...,c_m} est l’ensemble des m contraintes.

Les contraintes peuvent être exprimées sous différentes formes : table de valeurs compatibles, formules mathématiques, etc. Ce sont des relations entre des variables qui définissent la structure du problème à résoudre.

Définition 2 [Contrainte] Soit un CSP (X,D,C), une contrainte c ∈ C sur les variables x_i₁,...,x_{i_k} pour i₁,...,i_k ∈ {1,...,n} est une relation dans D_{x_i₁} ×...×D_{x_{i_k}}, domaines des variables x_i₁,...,x_{i_k}. On a donc :

c ⊆ ∏_j=i₁^i_k D_{x_j}

On note var(c), l’ensemble des variables intervenant dans la contrainte c.
Définition 3 [Arité] L’arité d’une contrainte c ∈ C est le nombre de variables sur lesquelles elle porte (i.e. le cardinal de var(c)). On dira que la contrainte est :

unaire si son arité est égale à 1,

binaire si son arité est égale à 2,

n-aire si son arité est égale à n.

Pour écrire de telles contraintes de manière formelle, on se fixe un langage. Dans ce langage du premier ordre, on retrouve naturellement les symboles des variables (x,y,x₁, X,Y etc), des fonctions (arithmétique +,-,*,/, booléennes ∧ ,∨, ⌉) et des relations (=, < , > , ≠ , ≥ , ≤ , ⇒,⇔ ).

nbr@exemples1

Exemple (CSP simple) :

Nous pouvons, par exemple, définir un problème simple sous forme de CSP (X,D,C) avec :

X = {a,b,c,d},
D_a = D_b = D_c = D_d = {0,1},
C = { a ≠ b, c ≠ d, a+c < b }.

Ce CSP comporte 4 variables a, b, c et d, chacune pouvant prendre 2 valeurs (0 ou 1). Une solution possible pour ce problème est a=0, b=1, c=0 et d=1.

Étant donné un CSP (X,D,C), sa résolution consiste à affecter des valeurs aux variables, de telle sorte que toutes les contraintes soient satisfaites. On introduit pour cela les notations et définitions suivantes.

Définition 4 [Affectation] Soit un CSP (X,D,C), on appelle affectation le fait d’instancier certaines variables par des valeurs (prises dans leurs domaines respectifs). Une affectation est une fonction :

s : X → n
∏
i=1
D_{x_i}

telle que s(x_i) ∈ D_{x_i} pour i ∈ [1..n].
Pour simplifier, on notera s = (d₁,d₂,..., d_n) une affectation des variables avec la valeur d₁ pour la variable x₁, d₂ pour la variable x₂,..., d_n pour la variable x_n.

Dans l’exemple 1, s=(0,1,0,1) est l’affectation qui instancie a à 0, b à 1, c à 0 et d à 1.
Une affectation est dite totale si elle instancie toutes les variables du problème ; elle est dite partielle si elle n’en instancie qu’une partie.
D’autres définitions sont nécessaires pour énoncer les principales caractéristiques des CSP ; nous devons définir les notions de solution et d’espace de recherche. Nous terminerons par représentation graphique d’un problème.

Définition 5 [Espace de recherche] L’espace de recherche d’un CSP P = (X, D, C) est l’ensemble des affectations possibles que l’on notera S.

S = D_x₁ ×D_x₂ ×... ×D_{x_n}

Avec D = { D_x₂, ... , D_{x_n} }.
L’espace de recherche est égal au produit cartésien de l’ensemble des domaines des variables et une affectation s sera assimilée à un élément de cet ensemble S (i.e. s=(d₁,...,d_n)).
Une affectation s ∈ S satisfait une contrainte c_k ∈ C si toutes les variables de var(c_k) sont instanciées par s et si la relation définie par c_k est vérifiée pour les valeurs des variables de var(c_k) données par s. Pour simplifier, on notera : s ∈ c_k.

Sur notre exemple 1, l’affectation complète s = (0,0,0,0) viole la contrainte a ≠ b.

Définition 6 [Solution] Une solution d’un CSP P = (X, D, C) est une affectation s ∈ S qui satisfait toutes les contraintes. On note Sol(P) l’ensemble des solutions.

Sol(P) = { s ∈ S | ∀c ∈ C, s ∈ c }

L’ensemble des solutions correspond à tout élément de l’espace de recherche (affectations) appartenant aussi aux valeurs permises pour chaque contrainte.
Définition 7 [Graphe et hyper-graphe de contraintes]
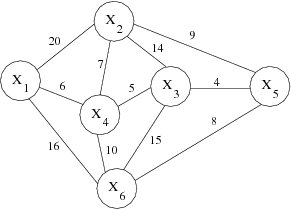
A chaque CSP P = (X, D, C) peut être associé, pour les contraintes binaires, un graphe des contraintes (ou graphe associé) obtenu en représentant chaque variable du réseau par un sommet et chaque contrainte binaire qui porte sur les variables x_i et x_j, notée c_ij ∈ C par une arête entre les sommets x_i et x_j. Dans le cas des CSP à avec des contraintes n-aires, on peut utiliser la représentation par hyper-graphe, en remplaçant les arêtes par des hyper-arêtes.
Le graphe des contraintes permet d’avoir un rendu graphique du problème ; il se trouve ainsi être parfois l’intermédiaire entre le problème réel et sa transcription dans le formalisme CSP. C’est le cas par exemple pour le problème de coloriage de graphe qui sera présenté dans la section suivante.

1.3 Les problèmes d’optimisation
sous contraintes

Un problème d’optimisation sous contraintes consiste à trouver une solution optimale parmi l’ensemble des solutions réalisables (i.e qui ne violent pas de contraintes). Le problème est alors double, nous avons : d’une part une recherche des solutions réalisables et d’autre part une recherche d’une solution optimale. Une fonction, appelée fonction objectif, est définie selon le problème posé pour évaluer la qualité d’une affectation. Cette fonction associe à chaque instanciation une valeur, l’objectif est alors de trouver l’affectation qui minimise ou maximise cette fonction.

Définition 8 [Problème d’optimisation sous contraintes] Étant donné un CSP P = (X,D,C), notons S l’espace de recherche défini par les domaines de D.
Soit (K, < ) avec K un ensemble totalement ordonné par la relation stricte < et f une fonction de coût, aussi appelé fonction objectif de S vers K :

f :
S → K

s → k

On définit alors un problème d’optimisation sous contraintes comme la minimisation (resp. la maximisation) de f, le but est alors de trouver une solution réalisable (i.e. s ∈ Sol(P)) ayant la plus petite valeur k (resp. la plus grande) par f. De manière plus formelle :

s ∈ Sol(P) t.q. ∀s’ ∈ Sol(P), f(s’) ≥ f(s) (resp. f(s’) ≤ f(s))

1.4 Exemples de formalisation

Comme suggéré en début de chapitre, une multitude de problèmes se modélisent sous forme de CSP. Dans ce qui suit nous rappellerons des problèmes simples, i.e., académiques.

1.4.1 Le problème du coloriage
de carte

Le problème de coloriage de carte, cas spécial du coloriage de graphe, peut se modéliser sous forme de CSP. Dans ce problème, nous devons colorier (avec un ensemble de couleurs donné) chaque région d’une carte, c’est à dire d’un graphe planaire, de telle manière que deux régions adjacentes n’aient pas la même couleur.

La figure 1.1 montre un exemple de problème du coloriage de carte et son équivalent CSP sous la forme du graphe des contraintes. La carte comporte quatre régions devant être coloriées en rouge, bleu ou vert. Le CSP équivalent a une variable pour chacune des quatre régions. Le domaine de chaque variable correspond à l’ensemble des couleurs. Pour chaque paire de régions adjacentes, une contrainte binaire est créée entre les variables correspondantes. Cette contrainte interdit toute affectation identique de ces deux variables.

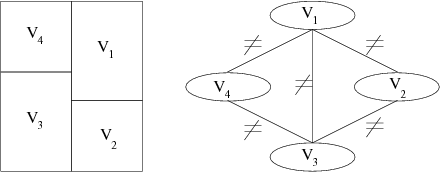
Figure 1.1: Exemple de problème de coloriage de carte et son équivalent en problème de satisfaction de contraintes

Plus formellement :

X = {V₁,V₂,V₃,V₄}
D = { D_V₁,D_V₂,D_V₃,D_V₄} avec D_{V_i} = {Rouge, Vert, Bleu}
C = { V₁ ≠ V₂ ; V₁ ≠ V₄ ; V₂ ≠ V₃ ; V₃ ≠ V₄}

1.4.2 Le placement de reines

Le problème des n reines consiste à placer n reines sur un échiquier n ×n de sorte qu’aucune reine ne soit en prise avec une autre. Ceci revient à placer au plus une reine par ligne, par colonne et par diagonale.

Figure 1.2: Une solution pour le placement de 8 reines sur un échiquier

En exploitant le fait qu’une seule reine sera placée par colonne, le problème se réduit au choix de la ligne. En conséquence de quoi, une modélisation du problème considère chaque colonne i comme une variable X_i qui désigne le numéro de ligne où se place la reine située en colonne i.

Si l’on se place dans le cadre général avec n reines :

X = {x₁,x₂, ..., x_n}
D = { D_x₁,D_x₂,..., D_{x_n} } avec D_{x_i} = {1,2,...,n}
C est défini par, ∀i, ∀j : les reines doivent être sur des lignes différentes x_i ≠ x_j, les reines doivent être sur des diagonales différentes x_i +i ≠ x_j +j, x_i - i ≠ x_j - j

Une solution du problème des 8 reines est illustrée en figure 1.2.

1.4.3 Le problème du Zèbre

Le problème du Zèbre est un puzzle logique qui figure lui aussi parmi les classiques du genre, il se pose comme suit :
Cinq maisons de couleurs différentes sont habitées par cinq personnes de nationalités distinctes, ces personnes ont leurs boissons préférées, leurs animaux domestiques et leurs sports pratiqués eux aussi différents. Les informations dont nous disposons sont les suivantes :

l’anglais habite la maison rouge,
l’espagnol a un chien,
la personne dans la maison verte boit du café,
l’irlandais boit du thé,
la maison verte est à droite de la maison ivoire,
le joueur de Go possède un escargot,
la personne dans la maison jaune joue au cricket
la personne dans la maison du milieu boit du lait,
le nigérien habite la première maison,
le judoka habite à côté de la personne qui a un renard,
le joueur de cricket est à côté de celui qui a un cheval,
le joueur de poker boit du jus d’orange,
le japonais joue au polo,
le nigérien habite à côté de la maison bleue.

La question est alors la suivante : Qui possède le zèbre et qui boit de la Guinness ?

Le problème est modélisé en numérotant les maisons de gauche à droite, de 1 à 5. Chaque couleur, personne, chose, animal, sport, boisson constitue une variable dont le domaine contient initialement les nombres de 1 à 5. Ainsi, si la couleur bleue est instanciée par la valeur 3, cela signifie que la maison 3 est bleue. Soit la liste des variables de taille 5 suivante, rangées par catégorie :

Anglais, Espagnol, Irlandais, Nigérien, Japonais,
Rouge, Verte, Bleue, Ivoire, Jaune,
Chien, Escargot, Renard, Zèbre, Cheval,
Judo, Go, Cricket, Poker, Polo
Lait, Guinness, Café, Thé, Jus,

La liste des contraintes :

Anglais = Rouge,
Espagnol = chien,
Verte = Café
Irlandais = Thé,
Verte = Ivoire + 1
Go = Escargot,
Cricket = Jaune,
Lait = 3,
Nigérien = 1,
| Judo - Renard | = 1,
| Cricket - Cheval | = 1,
Poker = Jus,
Polo = Japonais
| Nigérien - Bleue | = 1,

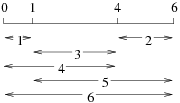
1.4.4 La règle de Golomb

Le problème de Golomb consiste à placer N marques sur une règle pour que toutes les distances entre les marques soient différentes, la figure 1.3 illustre le placement de quatre marques.

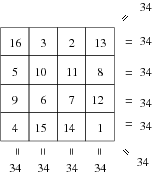
Figure 1.3: Solution d’une règle de Golomb à 4 marques

Les règles du professeur de mathématiques Solomon W. Golomb suscitent un intérêt particulier et l’aspect combinatoire de ce problème est encore aujourd’hui étudié, comme le montre les travaux de [ Meyer and Jaumard2006].

1.4.5 Les carrés magiques

Un carré magique d’ordre n est une matrice de n×n contenant tous les nombres de 1 à n² placés pour que chaque ligne, chaque colonne et les deux diagonales aient la même somme.

Figure 1.4: Carré magique d’ordre 4

Dans la figure 1.4 cette somme est de 34. Le CSP équivaut à un problème d’ordre 3, à 9 variables de taille 9, pour chaque élément de la matrice. Les contraintes sont alors les sommes de chaque ligne colonne et diagonale, soit 6+2 contraintes.

1.4.6 SEND + MORE = MONEY

Ce puzzle de cryptarithmétique consiste à retrouver les chiffres cachés derrière les lettres de cette addition 1.5.

Figure 1.5: Quels sont les chiffres associés aux lettres S E N D M O R Y?

Ce qui revient au calcul suivant :

	1000 ×S + 100 ×E + 10 ×N + D
+	1000 ×M + 100 ×O + 10 ×R + E
=	10000 ×M + 1000 ×O + 100 ×N + 10×E + Y

Une formulation en CSP de ce problème peut considérer chaque lettre S, E, N, D, M, O, R, Y comme une variable. Á chaque variable, les valeurs possibles correspondent aux chiffres de 0 à 9 et l’objectif est donc de trouver la valeur de chaque variable pour satisfaire l’addition.

1.4.7 Le nombre de Langford

Ce problème consiste à placer deux ensembles de chiffres (de 1 à 4) dans un certain ordre de sorte que les 2 1 soient séparés par un chiffre, les 2 2 , par 2, etc. Le problème se généralise alors sous la forme LN(k,n), avec k ensembles comportant chacun les nombres de 1 à n.

Figure 1.6: Solution du nombre de Langford (2,4)

Les figures 1.6 et 1.7 représentent une solution du problème avec deux ensembles de quatre chiffres et pour trois ensembles de neuf chiffres. Mais la complexité du problème augmente très vite avec la taille, ce qui nécessite des calculs énormes, comme le montre [ Krajecki et al. 2005].

Figure 1.7: Solution du nombre de Langford (3,9)

Une formalisation en CSP comprend, pour le problème LN(2,4), 8 variables indexées de x₁ à x₈. Le domaine de chaque variable correspond aux places que peut prendre la variable dans la séquence. Les contraintes se définissent alors comme suit :

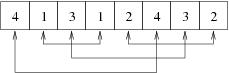
| x₁ - x₂ | = 2
| x₃ - x₄ | = 3
| x₅ - x₆ | = 4
| x₇ - x₈ | = 5
x₁ ≠ x₂ , x₁ ≠ x₃, x₁ ≠ x₄, x₁ ≠ x₅ , x₁ ≠ x₆ , x₁ ≠ x₇ , x₁ ≠ x₈ , x₂ ≠ x₃ , x₂ ≠ x₄ , x₂ ≠ x₅ , x₂ ≠ x₆ , x₂ ≠ x₇ , x₂ ≠ x₈ , x₃ ≠ x₄ , x₃ ≠ x₅ , x₃ ≠ x₆ ,x₃ ≠ x₇ , x₃ ≠ x₈ , x₄ ≠ x₅ , x₄ ≠ x₆ , x₄ ≠ x₇ , x₄ ≠ x₈ , x₅ ≠ x₆ , x₅ ≠ x₇ , x₅ ≠ x₈ ; x₆ ≠ x₇ ; x₆ ≠ x₈ ; x₇ ≠ x₈

Cachée derrière cet ensemble d’inégalités se trouve une contrainte globale de type Alldiff. Les contraintes globales sont très utiles dans certains cas de figure car elles simplifient non seulement la rédaction des contraintes et leurs interprétations mais permettent aussi d’améliorer la résolution par des algorithmes spécifiques [ Régin1994]. Dans cet exemple l’ensemble des inégalités se resume à la contrainte AllDif traduisant le fait que toutes les variables doivent prendre des valeurs différentes.

1.4.8 Le voyageur de commerce

Un exemple classique d’optimisation sous contraintes est celui du voyageur de commerce, celui-ci doit traverser n ville, l’objectif est donc de trouver le meilleur chemin, le plus court, passant par ces villes (voir figure 1.8). Le problème se modélise en CSP de manière intuitive avec n ville et les distances entre les villes notées δ_{x_i,x_j} (distance entre la ville i et et la ville j) :

X = {x₁,x₂, ..., x_n}
D = { D_x₁,D_x₂,..., D_{x_n} } avec D_{x_i} = {1,2,...,n}
C est défini par, une contrainte AllDiff(x₁,...,x_n) traduisant le fait que nous devons passer une seule fois par ville et par toutes les villes.
f = min(å_i=1^n-1 δ_{x_i,x_i+1})

Figure 1.8: Pouvons nous trouver un chemin qui partant de x₂ qui passe par tous les sommets et ce pour un coût inférieur 40 : La solution x₂, x₄, x₆, x₅, x₃, x₄, x₁ semble adéquate.

1.5 Conclusion

Ce premier chapitre nous a permis d’introduire la notion de CSP et de souligner la simplicité de ce formalisme. Nous avons vu qu’un grand nombre de problèmes variés correpondent à des problèmes de satisfaction de contraintes.

Au travers des exemples, nous avons énoncé différents types de contraintes. Les contraintes arithmétiques avec des équations et inéquations mais aussi une contrainte globale. Outre la contrainte Alldiff, qui épargne l’écriture d’un ensemble d’inégalités, on retrouve dans cette catégorie, à titre d’exemple, les contraintes globales de cardinalité de type AtMost ou AtLeast.

Évidemment, un algorithme capable d’énumérer toutes les combinaisons possibles permet de résoudre tous les problèmes formulés en CSP, encore faut-il que le problème soit suffisamment petit pour que le programme termine en temps raisonnable, ce qui bien souvent n’est pas le cas. Dans les chapitres suivants, nous allons aborder les techniques de résolution de CSP.

Chapitre 2

Résolution des CSP par

des méthodes complètes

Ce chapitre présente les algorithmes de résolution de CSP utilisant une approche complète. Après avoir présenté les principes basiques de la recherche de solution, nous rappelons les propriétés de consistance liées aux contraintes. Ces propriétés témoignent de la structure du problème et leur utilisation permet de concevoir des algorithmes de résolution plus efficaces.

2.1 Introduction

La définition donnée d’un CSP permet de représenter un grand nombre de problèmes, comme rappelée au chapitre 1.2, et il n’existe pas de méthode universelle pour une résolution efficace. Diverses techniques ont été mises au point, notamment en utilisant les notions de consistance, que nous allons développer dans ce chapitre, ainsi que des combinaisons de ces méthodes pour former des algorithmes de résolution.

Étant donné un CSP, un solveur a pour objectif de fournir les solutions satisfaisant les contraintes dans la mesure où cela est possible. Les propriétés des solveurs peuvent s’énoncer ainsi :

Un solveur est complet s’il est toujours capable de répondre par vrai ou faux concernant l’existence d’une solution.
Un solveur est correct s’il ne calcule que des solutions.
Un solveur est fiable s’il calcule toutes les solutions pour un problème donné.

Dans un cas idéal, l’exécution d’un solveur doit se terminer en un temps fini, fournir toutes les solutions, satisfaisant bien sûr toutes les contraintes. Pour éviter de tester toutes les combinaisons variable-valeur inhérentes à la formulation d’un CSP, la plupart des approches utilisent le filtrage par consistance. Ce filtrage consiste à supprimer les valeurs des domaines ne pouvant satisfaire certaines contraintes et ainsi à réduire l’espace de recherche.

Dans ce chapitre, nous présenterons différentes méthodes pour la résolution des CSP par des algorithmes complets, de l’énumération de toutes les combinaisons possibles vers les méthodes plus élaborées : utilisation des consistances et d’algorithmes de filtrage dédiés à chaque type de contraintes. Nous présenterons les propriétés de consistance et nous verrons dans quelle mesure elles sont transcrites en terme d’algorithmes.

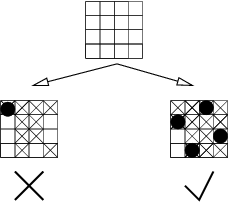
2.2 Generate-and-test et backtracking

Une méthode simple pour la résolution des CSP est de générer toutes les configurations possibles, c’est à dire toutes les combinaisons possibles de valeurs des variables et de tester si elles vérifient les contraintes : auquel cas elles sont solutions. Cette approche est connue sous le nom de Generate-and-test.

Le nombre de possibilités testées est alors le cardinal du produit cartésien des domaines des variables, ce qui pour les problèmes de grandes tailles devient impossible à envisager.

Le backtracking est sans nul doute la méthode la plus répandue pour une recherche systématique. Pour cette méthode, les variables sont instanciées les unes après les autres et ce jusqu’à obtenir une affectation complète. Seulement, contrairement à un generate-and-test, cette méthode teste la faisabilité à chaque étape de la résolution, c’est-à-dire que pour chaque instanciation de variables, les contraintes dont les variables sont déjà instanciées sont vérifiées, sur l’affectation partielle courante .

Ainsi, lorsqu’à une étape donnée, l’affectation partielle courante viole une contrainte, le backtracking supprime le sous-espace de recherche en dessous du point de choix.

Figure 2.1: Arbre de recherche du backtracking

La figure 2.1 représente l’arbre de recherche du backtracking appliqué au problème des 4-reines (voir chapitre 1.4). Dans un premier temps, l’algorithme place la première reine en haut à gauche de l’échiquier, ensuite la deuxième reine ne trouve de place viable qu’en troisième ligne. La position de la 2 reine en troisième ligne rend impossible le placement d’une nouvelle, ce qui entraîne un retour sur sa position et la place en 4 ligne et ainsi de suite.

2.3 Notion de consistance

Comme notre objectif est de trouver une affectation pour chaque variable satisfaisant toutes les contraintes, l’idée est alors de réduire l’espace de recherche (l’espace des possibilités).

Pour ce faire, les algorithmes de résolution complets vont essayer de supprimer certaines valeurs dans les domaines, des valeurs dites inconsistantes. Une valeur est jugée inconsistante dans la mesure où elle n’est pas validé pour une ou plusieurs contraintes.

Une notion de consistance est donc à associer à la notion de contrainte. En effet, une contrainte force les variables à ne prendre que certaines valeurs, la consistance intervient là où des valeurs d’un domaine ne pourront en aucun cas satisfaire cette contrainte. La propriété de consistance pour une contrainte est atteinte lorsque plus aucune valeur ne peut être supprimée.

On considérera ici des propriétés de consistance locale, c’est-à-dire une consistance considérant chaque contrainte de manière indépendante.

Plusieurs formes de consistances sont alors à définir en fonction des caractéristiques des contraintes, c’est pourquoi, nous verrons dans un premier temps, les contraintes ne portant que sur une seule variable, avec les consistances de noeud, puis les contraintes à deux variables avec les consistances d’arc et enfin les consistances hyper-arc et la k-consistance pour les contraintes n-aires.

2.3.1 Consistance de noeud

Commençons cet examen des consistances par la consistance de n ud, celle-ci ne concerne que les contraintes unaires. Ce sont les contraintes les plus simples, car elles n’affectent qu’une seule variable.

Définition 9 [Consistance de noeud] On dit qu’un CSP est consistant de noeud si pour chaque variable x ∈ X, toute contrainte unaire partant sur x, coïncide avec le domaine de x. Soit un CSP (X,D,C) et c ∈ C :

var(c) = {x}

et

∀d ∈ D_x, d ∈ c

Exemple : CSP non consistant de noeud Considérons le CSP (X,D,C) où:

X = { x₁,...,x_n}
D = {D_x₁,...,D_{x_n}} avec ∀i ∈ [1..n] D_{x_i} = [1..10]
C = {x₁ ≥ 2,...,x_n ≥ 2}

Le CSP n’est pas consistant de noeud : les contraintes x_i ≥ 2 ne sont pas satisfaites par toutes valeurs des domaines.

Considérons maintenant une consistance pour les contraintes binaires.

2.3.2 Consistance d’arc

De manière informelle, une contrainte binaire est consistante d’arc si chaque valeur de chaque domaine appartient à au moins une paire de valeurs consistantes définie par la contrainte. On parle alors de CSP arc consistant si toutes ses contraintes binaires sont arc consistantes.

Définition 10 [Consistance d’arc] Soit un CSP (X,D,C), soit une contrainte binaire c ∈ C portant sur les variables x et y avec leur domaine respectif D_x et D_y, telle que c ⊆ D_x ×D_y. Nous dirons que c est arc consistante si :

∀a ∈ D_x, ∃b ∈ D_y, (a,b) ∈ c;

∀b ∈ D_y, ∃a ∈ D_x, (a,b) ∈ c.

Un CSP est arc consistant si toutes ses contraintes binaires sont consistantes.
Exemple : Consistance d’arc Considérons le CSP ne contenant que la contrainte x < y avec D_x = [5..10] et D_y = [3..7] figure 2.2. Ce CSP n’est pas arc consistant car en considérant la valeur 8 pour x, aucune valeur b dans D_y ne nous permet d’obtenir 8 < b.

Figure 2.2: CSP non consistant

Passons maintenant au cas plus général avec des contraintes d’arité supérieure.

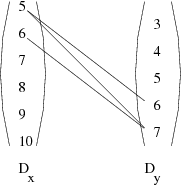2.3.3 Consistance hyper-arc

La notion de consistance hyper-arc généralise celle d’arc pour les contraintes n-aires.

Définition 11 [Consistance hyper-arc]
Soit un CSP (X,D,C), et une contrainte c ∈ C portant sur les variables x₁, x₂,...,x_n avec leur domaine respectif D_x₁,D_x₂,...,D_{x_n} de sorte que c ⊆ D_x₁ ×D_x₂ ×... ×D_{x_n}. On dit alors que c est hyper-arc consistante si pour chaque i ∈ [1..n] et a ∈ D_{x_i}, il existe un n-uplet d dans c de sorte que la i-ième composante de d soit égale à a.
Un CSP est hyper-arc consistant si toutes ses contraintes sont hyper-arc consistantes.
Une des faiblesses des consistances présentées est qu’elles considèrent les contraintes de manière isolée les unes des autres, ce qui leur confère l’aspect local, alors que dans la plupart des cas, elles partagent des variables.

2.3.4 La k-consistance

La k-consistance correspond à une généralisation des différentes notions vues jusqu’à présent et se définit ainsi :

Définition 12 [k-consistance]
Soit s une instanciation partielle de longueur k, i.e. k variables sont instanciées pour un CSP (X,D,C), si s satisfait toutes les contraintes, on dit alors que l’affectation est k-consistante.
Définition 13
Soit un CSP P, si pour toutes affectations partielles (k-1)-consistantes, pour chacune des autres variables non instanciées, il existe une valeur de leur domaine qui étend la consistance en une k-consistance, alors le CSP est dit k-consistant.
Un algorithme permettant d’établir la k-consistance a été présenté en 1989 par [ Cooper1989]. Nous pouvons donc faire correspondre cette notion avec les précédentes en appelant un CSP 1-consistant s’il est consistant de noeud, 2-consistant s’il est consistant d’arc.

2.4 Algorithmes de filtrage et propagation de contraintes

Nous avons présenté les propriétés de consistances et maintenant nous allons voir en quoi ces propriétés peuvent être utilisées pour la résolution des CSP par les méthodes complètes. Différents algorithmes sont définis pour assurer la consistance.

En introduisant les notions de consistance, il va de soi de présenter les algorithmes associés. L’objectif est alors d’atteindre la propriété de consistance locale en utilisant, en outre, la propagation de contraintes et le filtrage. Atteindre la propriété de consistance locale, pour un problème donné, simplifie la résolution en réduisant l’espace de recherche. Nous nous intéressons ici à des algorithmes complets, c’est à dire capables de nous répondre si le problème est insatisfiable.

Le filtrage des valeurs inconsistantes est utile pour instancier les variables et permet de retirer certaines valeurs des domaines tout en conservant les solutions. Les différents algorithmes de filtrages reposent bien sûr sur le type des contraintes exprimées.

L’objectif est de réduire les domaines pour rendre les CSP consistants relativement aux propriétés de chaque contrainte. L’algorithme associé aux contraintes unaires (procédure 1) est relativement simple, il se réduit à supprimer l’ensemble des valeurs ne satisfaisant pas la contrainte.

[!hbt]

#1Consistance de n ud()

Pour atteindre la consistance d’arc, il est nécessaire de vérifier les couples de valeurs possibles. La procédure Révise_arc, extraite de [ Mackworth1977], permet d’atteindre pour un arc donné, la propriété de consistance.

[!hbt]

#1Révise_arc(V_i,V_j)

Soit Supp un Booleen
Supp ← Faux

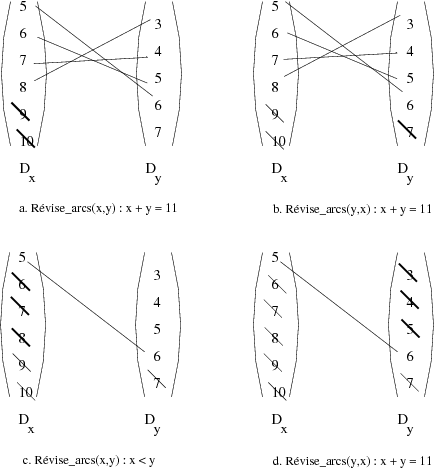
En ce qui concerne les contraintes binaires, pour faire en sorte que chaque arc soit consistant, une seule application de la procédure révise est insuffisante. En effet, la suppression d’une valeur d’un domaine pour une contrainte donnée peut avoir des répercussions sur les autres contraintes sur ce domaine.

Exemple : Révise_arc Pour l’exemple 2.2 considérons une deuxième contrainte. Rappelons que le CSP est défini par deux variables x, y avec D_x = [5..10] et D_y = [3..7]. Les contraintes sont c₁ : x > y et nous ajoutons c₂ : x+ y = 11. Le résultat de l’application des procédures Révise_arc est présenté par la figure 2.3. Nous remarquons dans cet exemple que la suppression de valeurs par c₁ en c. entraîne une autre application de la procédure pour c₂ en d. pour l’arc y,x bien qu’il soit déjà étudié en b.

Figure 2.3: Applications successives de la procédure Révise_arc

Pour propager les modifications apportées par une contrainte, des algorithmes ont été ainsi élaborés, ils permettent de tenir compte des modifications et de converger vers la propriété de consistance d’arcs pour l’ensemble des contraintes binaires du problème. Le premier d’entre eux, AC-1, tente de réviser systématiquement les contraintes en dépit du fait qu’ils ne soient pas affectés par une révision antérieure. Plus efficace que AC-1, Mackworth présente une variante, AC-3, qui utilise une queue pour ne revérifier que les contraintes dont l’un des domaines a été modifié évitant par là des tests inutiles. Suivent alors des algorithmes comme AC-4 [ Mohr and Henderson1986] pour palier à une redondance des testes liés à AC-3, AC-6 [ Bessière1994], AC-7 [ Bessière et al. 1999] pour une gestion des symétries, jusqu’à AC-2001 [ Bessière and Régin2001] capable de conserver des informations sur les variables testées et ainsi optimiser AC-3.

[!hbt]

#1AC-1()

Soit Q l’ensemble des arcs du graphe des contraintes G;
Q ← {(V_i,V_j) ∈ arcs(G), i ≠ j};
Soit CHANGE un Booleen

[!hbt]

#1AC-3()

Soit Q l’ensemble des arcs du graphe des contraintes G;
Q ← {(V_i,V_j) ∈ arcs(G), i ≠ j};
Soit CHANGE un Booleen

2.4.1 Les contraintes globales

Le filtrage des valeurs par arc-consistance est souvent insuffisant car il ne tient pas compte des liens existant entre les contraintes. Pour être plus efficace, des contraintes globales ont été introduites, celles-ci parfois correspondent à es conjonctions de plusieurs contraintes. Un algorithme de filtrage est alors dédié à la contrainte pour un meilleur filtrage. La première et la plus célèbre est la contrainte globale de type Alldiff (conjonction de contraintes de différence), une procédure permet de filtrer les domaines à condition qu’au moins un domaine se résume à une seule valeur.

Exemple : CSP avec contrainte Alldiff
Considérons le CSP (X,D,C) où:

X = { x₁, x₂, ,x₃}
D = {D_x₁,D_x₂,D_x₃} avec D_x₁ = {1}, D_x₂ = {1;2} et D_x₃ = {2;3}
C = { AllDiff(x₁,x₂,x₃)}

Le CSP 3 contient une seule contrainte de type AllDiff et une affectation des variables qui satisfait cette contrainte est x₁ = 1, x₂ = 2 et x₃ = 3.

[htb]

#1AllDiff(S)

Soit S un ensemble de variables

Les avantages apportés par une modélisation avec des contraintes globales ne se limitent pas à des procédures de filtrage spécifiques. On retrouve également des procédures de vérification capables de prouver l’inconsistance d’un problème (voir exemple 4).

Exemple Vérification pour AllDiff

Considérons le CSP (X,D,C) avec :

X = { x, y , z}
D = {D_x,D_y,D_y} avec D_x = D_y = D_x = {1;2}
C = { x ≠ y , x ≠ z , y ≠ z }

Ce CSP contient trois contraintes, toutes sont arc consistantes. Ces trois contraintes sont équivalentes à la contrainte AllDiff(x,y,z). Or une procédure de vérification de AllDiff détectera que ce problème, bien qu’il soit arc consistant, n’est pas consistant. Car le cardinal de l’union des domaines (card(D_xUD_y UD_z) = 2) est inférieur au nombre de variables (card(D) = 3).

2.5 Méthodes de recherche et algorithmes de résolution

Après avoir présenté le backtrack, le filtrage et la propagation de contraintes, nous sommes en mesure de définir des algorithmes complets pour la résolution de CSP.

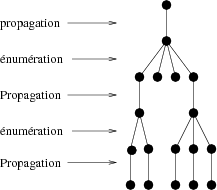
Dans un premier schéma, la résolution se résumait à instancier les variables les unes après les autres tout en testant si elles ne violent pas de contraintes. Nous pouvons à présent utiliser les consistances et propager pour réduire l’espace vers un problème plus simple à résoudre à chaque n ud et ainsi limiter les points de choix. En général, un algorithme de backtrack standard en profondeur d’abord est appliqué avec, à chaque n ud de l’arbre de recherche, une propagation de contrainte à des niveaux plus ou moins élevés selon les méthodes (voir figure 2.4) et comme aucune solution n’est perdue pendant la recherche, la résolution reste complète. Le backtrack a pour but une énumération des valeurs des variables (voir chapitre 2.2) avec à chaque étape un choix a effectuer sur la variable qui sera énumérée ainsi que sur les valeurs choisies.

Figure 2.4: Arbre de recherche : propagation + énumération

Dans [ Kumar1992] un récapitulatif adapté de [ Nadel1988] énonce un certain nombre d’algorithmes en les identifiant par un degré d’utilisation des méthodes de consistances à chaque n ud de l’espace de recherche. Un grand nombre d’algorithmes suit ce format [ Haralick and Elliott1980, Fikes1970, Ullmann1976, Haralick et al. 1978, McGregor1979, Dechter and Meiri1989].

Figure 2.5: Arbre de recherche du Forward Checking

Nous retrouvons le Generate and Test(GT) qui n’utilise pas la notion de consistance jusqu’au Really Full Look Ahead capable de maintenir la consistance d’arc dans le backtrack. Les stratégies se différencient dans les choix opérés lors des phases de propagations et d’énumérations. Pendant le parcours de l’arbre de recherche (vois figure 2.4), elles conservent l’aspect complet et préservent les solutions.

Nous nous limiterons à quelques méthodes illustrées par le problème du placement des reines, à commencer par le Forward Checking.

Figure 2.6: Arbre de recherche du Full Look Ahead

Dans l’exemple 2.5, avec un Forward Checking, à chaque instanciation d’une variable, les conséquences à court terme sont propagées sur les autres domaines. Une reine est placée en haut à droite de l’échiquier, les contraintes impliquant cette reine sont alors utilisées et suppriment la possibilité de placer la seconde dans les 2 premières lignes. Placer la seconde reine en 3 ligne supprime toute possibilité pour la 3 reine donc retour à la case départ, etc. Le Full Look Ahead lui, ne se contente pas d’une seule propagation, mais étend la consistance sur l’ensemble des variables. C’est alors que comme le montre la figure 2.6, dès le placement de la première reine aucun arc de valeurs consistantes ne subsiste liant la deuxième variable aux autres.

2.6 Conclusion

Nous avons vu que les propriétés des contraintes sont utiles pour réduire l’espace de recherche, et que le backtrack et les propriétés de consistance locale permettent une résolution complète d’un problème.

Par une propagation des contraintes (à des degrés différents) et différentes stratégies de parcours de l’arbre de recherche (le plus commun étant en profondeur d’abord), un simple backtracking se transforme alors en un solveur parfois assez complexe. Seulement ce mode de résolution semble atteindre ses limites pour certains problèmes où les contraintes ne permettent pas de réduire un espace de recherche de manière significative et où un parcours complet de l’arbre des possibilités, malgré le filtrage, semble dès lors impossible. C’est dans ce contexte que les méthodes dites incomplètes ont émergé et feront l’objet du chapitre suivant.

Chapitre 3

Résolution des CSP par

des méthodes incomplètes

Les méthodes incomplètes (telles que la recherche locale (LS) [ Aarts and Lenstra1997]) reposent sur des heuristiques permettant d’étudier des zones spécifiques de l’espace de recherche dans le but d’atteindre une solution. Ce chapitre propose un panorama non exhaustif de ces méthodes.

3.1 Introduction

L’utilisation de métaheuristiques est apparue comme une issue face à des problèmes combinatoires dont les espaces de recherche explosent en taille. Pour les problèmes NP-difficiles, en admettant que P ≠ NP, il n’existe pas d’algorithme en temps polynomial et donc une résolution complète entraîne un temps de calcul exponentiel dans le pire des cas. Le développement récent de ces méthodes témoigne d’une part de l’intérêt que nombre de chercheurs y portent, mais aussi du potentiel de ces paradigmes de résolution. Les métaheuristiques sont basées sur deux concepts majeurs :

l’intensification consiste à fouiller une zone réduite de l’espace de recherche pour en extraire éventuellement une solution,
et la diversification qui permet à la recherche de se déplacer dans l’espace plus largement.

Ces notions vont définir le comportement des méthodes dans l’espace de recherche et nous verrons comment ces deux principes fonctionnent de la recherche locale jusqu’aux algorithmes génétiques. Les méthodes incomplètes sont principalement orientées vers l’optimisation d’une fonction d’évaluation sur l’ensemble des configurations. Ce qui pour les problèmes de satisfaction de contraintes correspond à une minimisation du nombre de contraintes violées pour des affectations complètes.

3.2 La recherche locale

Nombre de méthodes sont apparues combinant différentes heuristiques, ces combinaisons sont appelées métaheuristiques (dérivé du verbe grec heuriskein εuriskεin signifiant rechercher et du suffixe méta pour au niveau supérieur, au-delà de ). Ces méthodes considèrent l’espace de recherche dans sa totalité, l’ensemble des affectations possibles des variables. L’idée est donc, de ne pas visiter toutes ces configurations, mais de se doter d’heuristiques pour choisir les zones d’exploration. Les méthodes présentées correspondent à des schémas généraux qui leur confèrent le statut de métaheuristiques.

3.2.1 Recherche par voisinage

Le principe de base d’une recherche locale est de partir d’une configuration initiale (d’une affectation complète) et par un processus itératif, de remplacer la configuration courante par une meilleure prise dans ce qui est défini comme son voisinage. L’idée est donc d’être capable, si on améliore une configuration progressivement, d’atteindre une solution. En se déplaçant de proche en proche (s₀ → s₁ → ...) dans l’espace de recherche, la configuration courante est progressivement corrigée de ses défauts (dans notre contexte il s’agit de contraintes non satisfaites). Le voisinage représente des affectations autour de la configuration courante, accessibles en modifiant certains attributs (valeurs des variables) et est très souvent relatif au problème posé. Le voisinage se définit généralement comme suit :

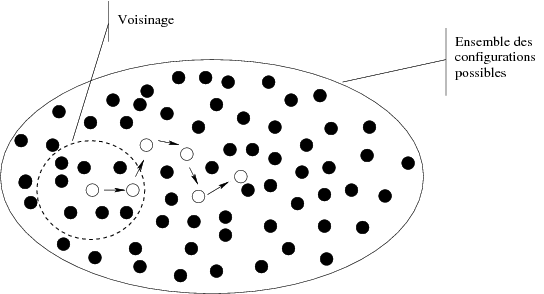
Définition 14 [Voisinage] Soit S un espace de recherche (appelé aussi espace des configurations), un voisinage est une fonction :

N : S → P(S)

qui associe à chaque élément s de l’espace de recherche S, un ensemble de voisins (élément de l’ensemble des parties P) N(s) ⊆ S. On appelle N(s) le voisinage de s.
Á partir de la configuration courante, le choix du voisin qui sera la prochaine étape de la recherche, se fait par une évaluation. La fonction d’évaluation eval témoigne de la qualité d’une configuration et, dans le contexte des problèmes de satisfaction de contraintes, est liée au nombre de contraintes violées.

eval :

S → ℵ

s → e

Cette fonction nous permet de diriger la recherche dans le voisinage à chaque itération.

Figure 3.1: Chemin de recherche locale

La figure 3.1 montre le chemin d’une recherche locale où la fonction d’évaluation des configurations complètes permet de sélectionner un voisin à chaque pas.

Un premier algorithme (3.1) consiste à sélectionner un voisin qui améliore la configuration courante. Le processus s’arrête dès qu’aucun élément autour de la configuration courante ne peut être choisi.

[htb] #1Descente Simple
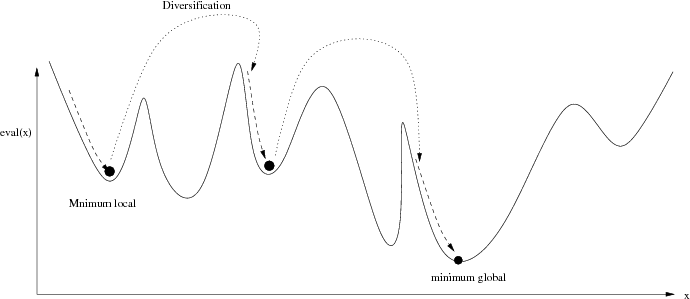
Soit x une configuration initiale prise aléatoirement

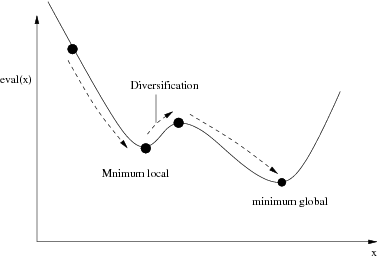
Le processus de descente simple se limite à une zone de recherche et ne permet pas de sortir des optimums locaux (figure 3.2).

Figure 3.2: Minimum local et global

Pour s’échapper de ses optimums locaux, une recherche locale intègre nécessairement un élément de diversification comme le montre l’algorithme 3.2. La diversification va permettre de se déplacer plus loin et d’explorer de nouvelles zones. Il peut s’agir d’un restart, c’est-à-dire d’une nouvelle recherche depuis un autre point initial ou d’un chemin aléatoire. Pour ce qui est de l’algorithme avec diversification qui est présenté, à chaque appel de l’algorithme de descente simple une configuration initiale est prise aléatoirement pour relancer la recherche. Le critère d’arrêt est laissé libre et peut être soit un nombre maximum d’itérations (cas le plus commun), soit un temps d’exécution maximum ou tout autre critère particulier lié au problème posé.

#1Descente Simple avec diversification
Soit x’ une configuration initiale et
x la meilleure solution trouvée avec eval(x) ← ∞

3.2.2 Algorithmes de recherche locale

Les algorithmes présentés sont à considérer comme des stratégies guidant la recherche basées sur le principe de voisinage, d’évaluation et de l’alternance des deux phases, à savoir intensification et diversification.

Le Recuit Simulé Simulated Annealing

Le recuit simulé est considéré comme la première métaheuristique pourvue d’une stratégie pour échapper aux minimums locaux. Son origine se trouve dans la description des phénomènes physiques en métallurgie. C’est dans [ Kirkpatrick et al. 1983] que ce processus est exploité pour la première fois pour la résolution des problèmes d’optimisation. Le principe de cette méthode est d’autoriser les déplacements vers des configurations de qualité moindre (que la courante) sous certaines probabilités. L’algorithme 3.3, dans ses grandes lignes, commence par s’initialiser avec une configuration complète et un paramètre température T. Pendant la recherche, la température T décroît selon une fonction de refroidissement qui influe sur les conditions d’acceptation d’une configuration en fonction de la dégradation qu’elle induit. Au début de la recherche, les configurations plus mauvaises sont acceptées facilement, en revanche au fur et à mesure que la recherche avance, la température T décroît ce qui réduit les chances d’acceptation pour une affectation de qualité moindre et permet d’assurer entre autre une certaine convergence de l’algorithme.

#1Recuit Simulé

Soit x une configuration initiale
Soit T une fonction de refroidissement et T une température initiale

Figure 3.3: Minimum local et Recuit Simulé

La figure 3.3 illustre un parcours dans lequel un minimum local est rencontré, mais dans lequel les configurations de qualité moindre sont tout de même acceptées ce qui permet de traverser cette zone pour retomber dans un minimum global.

Recherche Tabou

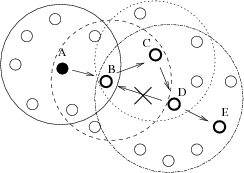
L’idée de base d’une recherche tabou a été introduite par [ Glover1986] sur des intuitions déjà présentes dans [ Glover1977]. Cette méthode est sans doute la plus populaire des métaheuristiques. Elle se base sur une descente avec sélection du meilleur voisin et sur une mémoire à court terme des précédentes configurations rencontrées, pour éviter les cycles (algorithme 3.4). Une liste est alors maintenue pour conserver la trace des affectations visitées et en interdire un nouveau passage. L’unique paramètre est la longueur l de cette liste.

#1Recherche tabou

Soit x une configuration initiale
Soit l une liste tabou dont la taille maximale est k

Dans la figure 3.4 la recherche débute en un point A de l’espace de recherche, quand la configuration D est atteinte, le mouvement de retour sur B est interdit ce qui contraint la recherche tabou à se diriger vers E en second choix.

Figure 3.4: Diversification avec une liste tabou

Ces méthodes appartiennent donc à une des deux grandes familles des métaheuristiques, la recherche locale. Une autre famille est celle des approches dites évolutionnistes avec les algorithmes génétiques.

3.3 Les algorithmes génétiques

Basés sur le principe de la sélection naturelle, les algorithmes génétiques [ Goldberg1989a, Holland1975a] ont été appliqués avec succès aux problèmes combinatoires tels que les problèmes d’ordonnancements ou de transports.

Le principe fondamental de cette approche est basé sur le fait que les espèces évoluent par adaptations à un environnement changeant et que le savoir acquis est inclus dans la structure de la population et de ses membres, codé dans leurs chromosomes. Les algorithmes évolutionnaires sont donc principalement basés sur la notion d’adaptation des individus d’une population, cette population évolue comme dans la théorie darwinienne, par des générations successives. Chaque nouvelle génération est généralement créée à partir de la précédente grâce à des opérateurs d’évolution comme le croisement de deux individus ou la mutation sur un gène d’un individu. Si des individus sont considérés en tant que solutions potentielles d’un problème donné (généralement un individu correspond à une affectation), l’application d’un algorithme génétique consiste en la génération successive de meilleurs individus. L’objectif est d’améliorer la qualité des individus, mesurée par une fonction d’évaluation, en faisant du croisement, une concaténation des meilleurs gènes des parents et de la mutation une amélioration de l’individu. Nous renvoyons le lecteur à [ Michalewicz1996] pour plus de détails.

Les populations

Un algorithme génétique comprend comme composant de base une population, c’est-à-dire un ensemble d’individus correspondant à une représentation des solutions potentielles. Dans la plupart des cas, un individu est un chromosome défini par ses gènes. Dans notre cas, un individu est une affectation de valeurs aux variables. Il est donc nécessaire que l’algorithme se dote d’un mécanisme de création d’une population initiale.

L’évaluation

Un autre élément à définir lorsque l’on conçoit ce type d’algorithme est la fonction d’évaluation. Cette fonction, que nous notons eval, évalue chaque solution potentielle selon le problème donné. Dans le cas des CSP cette fonction évalue le nombre de contraintes violées.

Les opérateurs génétiques

Les opérateurs génétiques définissent la génération des enfants pour la création de la population suivante. Deux opérateurs différents :

le croisement produit de nouveaux individus (les descendants) en croisant des individus de la population courante (les parents). Un exemple de croisement est donné en figure 3.5, il représente un croisement uniforme qui, à partir de deux parents x et y, créé un nouvel individu résultat de la recombinaison des gènes et qui sera ensuite inséré dans la population.

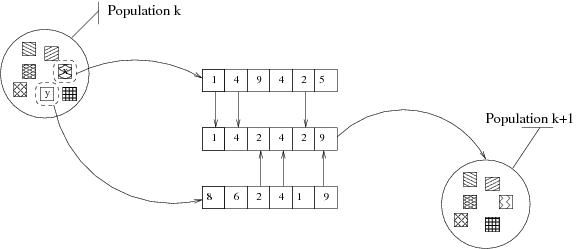
Figure 3.5: Exemple de croisement uniforme
la mutation, change arbitrairement un ou plusieurs gènes d’un individu choisi. La figure 3.6 nous montre comment, depuis un individu sélectionné dans une population k, un gène est muté dans k+1. Les mutations sont généralement utiles pour apporter de nouvelles informations. On peut très bien imaginer que, dans notre exemple, la valeur 8 n’apparaît dans aucun individu de la population k. La mutation dans ce cas introduit cette valeur et donc, ouvre la possibilité à de nouvelles configurations.

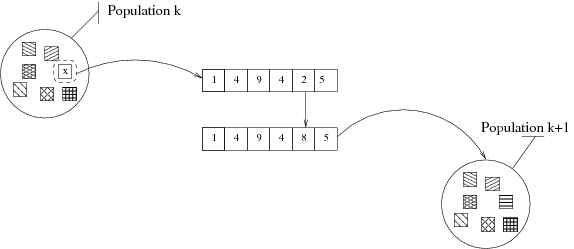
Figure 3.6: Exemple de mutation sur un gène

La sélection

Un dernier principe de base à définir est la sélection d’individus. L’objectif est de ne conserver que les meilleurs individus afin d’assurer une convergence globale. Nous pouvons retrouver ici le principe d’élitisme qui consiste à sélectionner la ou les meilleures configurations. Toutefois, cette opération de sélection se doit de préserver une certaine diversité dans la population, on y retrouve alors la mesure d’entropie pour une meilleure répartition des individus dans l’espace de recherche. Que ce soit pour la mutation ou pour le croisement, une sélection doit avoir lieu, dans la figure 3.7 des individus sont sélectionnés pour être soumis aux opérateurs de croisement ou mutation. De même, un ensemble d’individus est choisi pour constituer une nouvelle génération.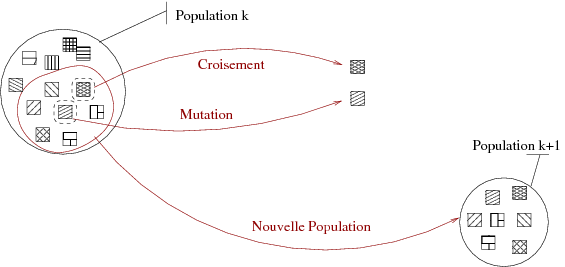

Figure 3.7: Exemple de sélections

Nous présentons un mécanisme général d’un algorithme génétique dans la figure 3.8. Ce schéma est loin d’être un modèle pour tous les algorithmes, mais présente néanmoins les éléments de base de cette méthode.

Figure 3.8: Mécanisme général des algorithmes génétiques.

Le bon fonctionnement d’un algorithme génétique dépend d’un grand nombre de paramètres. La gestion de la taille de la population, des probabilités de croisement et mutation, bref du compromis entre une exploitation (croisement) et une exploration (mutation, taille population) de l’espace de recherche.

3.4 Conclusion

Nous avons présenté les algorithmes pour les méthodes de recherches locales ainsi que le principe général qui régit un algorithme à base de population. Toutes ces méthodes s’appliquent à un grand nombre de problèmes différents et une métaheuristique constitue en quelque sorte un cadre qui s’adapte au problème posé. L’univers des méthodes incomplètes est vaste, beaucoup de méthodes ne sont pas présentées ici (Variable Neighborhood search[ Mladenovi\’c and Hansen1997], GRASP [ Feo and Resende1995], Idwalk [ Neveu et al. 2004]...). Elles donnent pour la plupart des clefs permettant de sortir des optimums locaux et ont prouvé leur efficacité sur des problèmes allant de la gestion de ressources réseaux aux problèmes d’affectation, en passant par la bioinformatique.

Bien qu’il s’agisse dans la plupart des cas de problèmes à base de contraintes, une structuration différente du problème est utilisée par les méthodes incomplètes vis à vis des méthodes complètes. Dans les premières (incomplètes), l’ensemble des affectations complètes est considéré tandis que dans l’autre, des affectations partielles sont construites incrémentalement. Cependant nous verrons par la suite, au travers d’exemples, qu’une hybridation peut s’avérer très efficace.

Chapitre 4

Résolution hybride

L’hybridation de méthodes complètes et incomplètes vise à profiter de leurs atouts respectifs en les fusionnant. La combinaison se fait soit au travers d’une collaboration de ces méthodes, soit par une intégration plus fine. Dans ce chapitre, nous dresserons un panorama des niveaux d’intégration et de collaboration pour des méthodes d’origines et de structures intrinsèquement différentes.

4.1 Introduction

Comme nous l’avons vu au chapitre 2, les méthodes complètes apportent des garanties en ce qui concerne l’obtention d’une solution optimale à un problème donné. L’inconvénient est que le temps de calcul augmente de façon exponentielle avec la taille des instances. Dans ce contexte, la garantie de l’optimalité est alors concédée vis-à-vis du temps de calcul.

Pour pallier ce sacrifice, une idée largement répandue pour la conception de solveurs plus efficaces et robustes, consiste à combiner plusieurs paradigmes de résolution, afin de bénéficier des atouts respectifs de chacun d’entre eux. ([ Focacci et al. 2002] dresse un panorama de telles utilisations de recherche locale (LS) dans la programmation par contrainte (CP)). Nous retrouvons alors des hybridations dans lesquelles la recherche locale est utilisée avec des mécanismes complets pour rendre les voisinages étendus plus intéressants [ Shaw1998]. Une autre méthode phare s’appuie sur la recherche locale afin de réparer des affectations partielles et utilise les techniques de filtrage [ Jussien and Lhomme2002].

Les bénéfices des combinaisons LS+CP sont bien connus, et [ Prestwich2000, Pesant and Gendreau1996] proposent des hybridations entre des méthodes de recherche locale et des techniques de propagation de contraintes.

Figure 4.1: Classification des combinaisons exactes/métaheuristiques

Les deux idées majeures utilisées pour mettre en place une combinaison de méthodes complètes et incomplètes sont, comme l’illustre la figure 4.1 :

la collaboration : on combine une méthode exacte et une métaheuristique exécutée en prétraitement et vice-versa. Les méthodes peuvent également fonctionner en parallèle tout en échangeant des informations.
l’intégration : une LS aide un algorithme complet : à quelques n uds de l’arbre de recherche, construits par l’algorithme de backtracking, la LS est utilisée pour tenter d’atteindre une solution, en partant d’une affectation partielle ou pour améliorer une configuration complète. La LS peut être ainsi considérée comme un mécanisme de réparation supplémentaire. Dans d’autres cas, la LS guide entièrement la recherche : la propagation de contraintes peut être utilisée pour limiter le voisinage ou élaguer des branches de l’espace de recherche. Des techniques complètes sont également utilisées pour explorer le voisinage de la configuration actuelle et choisir la prochaine étape du processus de LS.

4.2 Approches Collaboratives

Dans ce type de combinaison, les algorithmes proposés correspondent à une association de haut niveau entre métaheuristiques et méthodes complètes, (i.e. aucun algorithme n’est inclus dans un autre). Ainsi, la combinaison la plus répandue est l’utilisation en séquence.

La méthode exacte est soit exécutée comme un prétraitement, ou soit elle utilise la métaheuristique.

Dans [ Applegate et al. 1998] une méthode est proposée pour l’obtention de solutions quasi optimales du problème du voyageur de commerce. Un ensemble des solutions est extrait via des exécutions d’une recherche locale itérative. Les ensembles d’arêtes sont réunis et le problème se réduit au calcul de l’optimum sur un graphe largement simplifié. De cette façon, la solution obtenue est habituellement meilleure que la meilleure des solutions de la recherche locale.

Beaucoup de problèmes d’optimisation possèdent une certaine structure, c’est-à-dire les configurations de bonnes qualités ont un grand nombre de caractéristiques communes avec les solutions optimales. Cette observation peut être exploitée de plusieurs manières en définissant des sous-problèmes appropriés vis-à-vis du problème original. Dans la plupart des cas, les sous-problèmes résultants sont suffisamment petits pour être résolus par une méthode exacte.

Ce type d’approche se décompose en deux phases. Dans une première, un algorithme approximatif est utilisé pour collecter des solutions du problème considéré. Basé sur la composition des solutions, un sous problème est défini. Il est alors nécessaire que le sous problème généré contienne si ce n’est toutes, au moins la plupart des variables de décisions importantes , et qu’il se résolve facilement.

Les grandes lignes pour cette méthode sont présentées par 4.1.

[!hbt]

#1Exploiter la structure par collecte d’informations

Parfois, une version relaxée du problème original est résolue de façon optimale et les solutions obtenues sont réparées pour constituer les points de départ d’une métaheuristique. La relaxation en programmation linéaire (PL) est souvent utilisée dans ce but. Par exemple, [ Feltl and Raidl2004] résolvent le problème d’affectation généralisé, avec un algorithme génétique hybride : la relaxation PL du problème est traitée par CPLEX et ses solutions fournissent une population d’individus qui seront, si besoin est, soumis à des opérateurs de réparation pour constituer la population initiale.

Une autre approche de type séquentiel est celle d’un B&B couplé à un AG décrit dans [ Nagar et al. 1995] où les solutions du problème d’ordonnancement flow-shop (ou atelier en ligne) avec deux machines sont représentées en tant que permutation des tâches. Avant l’application de l’AG, un B&B est utilisé jusqu’à une certaine profondeur k et les bornes calculées sont enregistrées à chaque n ud de l’arbre B&B. Pendant l’exécution de l’algorithme génétique, les solutions partielles jusqu’à une certaine position k, sont mises en correspondance sur leur n ud associé de l’arbre. Si les bornes indiquent qu’aucun chemin qui suit le n ud, ne mène à une solution, la configuration subit alors une mutation.

4.3 Approche intégrative

Cette fois, la combinaison est plus fine, dans une approche intégrative les méthodes sont plus étroitement liées.

4.3.1 La recherche locale au secours de l’algorithme complet

L’efficacité d’une méthode complète réside aussi bien dans le choix de la variable à instancier et de la valeur de cette instanciation que dans les outils dont elle se dote pour établir la consistance.

Métaheuristique pour l’obtention de bornes

Des heuristiques permettent d’établir un ordre sur les variables à instancier afin de réduire l’arbre de recherche et de retarder le backtrack.

Elles indiquent l’ordre des valeurs le plus approprié pour trouver une solution plus rapidement ou anticipent le fait que l’affectation partielle courante ne permette pas d’atteindre une solution.

Dans le formalisme CSP, avec des contraintes impératives, l’objectif est de trouver une affectation des variables ne violant aucune contrainte. Dans ce contexte, les méthodes incomplètes sont très efficaces, pas trouver une solution directement, ou pour minimiser le nombre de contraintes violées et fournissent alors une borne supérieure suffisamment précise pour un algorithme de type branch and bound. Par exemple, [ Woodruff1999] présente une stratégie de sélection chunking based pour décider des n uds dans l’arbre de B&B où sera appelée la procédure tabou réactive, laquelle pourra trouver une solution. Cette stratégie mesure la distance entre le n ud courant et les n uds déjà explorés par une métaheuristique pour influer sur la sélection. Les expérimentations montrent que l’ajout de métaheuristiques améliore les performances du B&B.

Affaiblissement des méthodes complètes

La notion d’affaiblissement intervient dès lors qu’une méthode perd sa complétude. Les raisons, qui contraignent l’exploration à élaguer certaines branches de l’arbre de recherche, peuvent être liées à un temps d’exécution limité ou la décision de concentrer la recherche sur une zone jugée plus intéressante et prometteuse. C’est justement, dans ce type de décision qu’interviennent des heuristiques, et de façon plus globale, les méthodes incomplètes.

Certaines méthodes consistent, sur la base d’une heuristique, à supprimer certains n uds. Par exemple, [ Ginsberg and Harvey1990] présente un algorithme appelé iterative broadening. Dans cet algorithme un chemin est initialement proposé par une heuristique. Les domaines des variables sont ainsi réduits à une seule valeur. Puis de manière incrémentale, à chaque fin d’exploration d’un problème simplifié, on réalise une réduction moins forte des valeurs des domaines, en prenant en compte les i premières valeurs des domaines.

Limited Discrepancy search (LDS) [ Harvey and Ginsberg1995] est un algorithme de recherche qui limite l’effort de recherche dans des régions de l’arbre jugées plus prometteuses pour trouver une solution.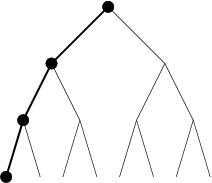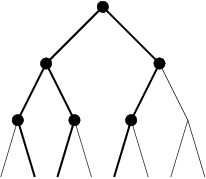


discrepancy 0	discrepancy 1

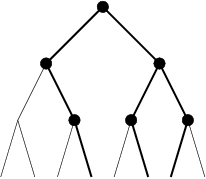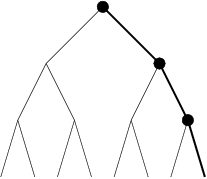discrepancy 2	discrepancy 3

Figure 4.2: Processus de recherche LDS

Le processus de recherche choisit dans un premier temps, les meilleurs n uds en fonction d’heuristiques données à chaque point de décision (ce que l’on nomme la recherche discrepancy 0).

Si aucune solution n’a pu être trouvée, avec une discrepancy 0, le processus de recherche permet de sélectionner un autre sous-n ud à chaque point de décision (discrepancy 1).

Si une solution ne peut être atteinte, la recherche se fait ensuite par augmentation des n uds visités de façon incrémentale (discrepancy 2, discrepancy 3).

La figure 4.2 nous montre les chemins parcourus par une recherche LDS sur un arbre binaire de profondeur 3. Supposons que l’heuristique mise en uvre ordonne les n uds de gauche à droite, avec une (discrepancy 0) la recherche sélectionne le n ud gauche à chaque point de décision. L’ensemble des chemins possibles est alors emprunté à la (discrepancy 3).

4.3.2 Une méthode complète au c ur du voisinage d’une recherche locale

Nous considérons ici les techniques dans lesquelles des algorithmes exacts sont incorporés dans des métaheuristiques.

Recherche exacte et voisinage large

Une idée assez répandue consiste à explorer les voisinages, dans une métaheuristique à base de recherche locale, au moyen d’algorithmes exacts.

Si le voisinage est choisi de façon appropriée, il peut être de grande taille. Néanmoins, une recherche efficace saura trouver le meilleur voisin. Ces techniques sont connues sous le nom de Very Large-Scale Neighborhood (VLSN) search [ Ahuja et al. 2002].

L’idée centrale, dans ce type d’algorithme combinant recherche locale et méthodes exactes, est de modéliser le problème d’une recherche dans un grand voisinage comme un problème d’optimisation, lequel est résolu par une méthode exacte. La solution obtenue remplace alors la solution courante de la recherche locale. Un algorithme général d’une telle méthode peut se décrire par l’algorithme 4.2

[!hbt]

#1Recherche dans un voisinage

Une autre possibilité est que seule une partie du voisinage soit examinée à chaque étape de recherche locale. Ce qui se fait classiquement lorsqu’une partie de la solution courante est conservée, définie comme solution partielle, et que les autres variables de décision sont laissées libres.

L’algorithme 4.3 présente une vue d’ensemble d’une telle procédure.

[!hbt]

#1Recherche partielle dans un voisinage

[ Burke et al. 2001] présente une recherche locale avec voisinage variable pour le problème du voyageur de commerce, dans laquelle les auteurs insèrent un algorithme exact dans la partie recherche locale, appelée HyperOpt, dans le but de rechercher de manière exhaustive de larges, mais prometteuses régions de l’espace des solutions.

De plus, ils proposent une hybridation HyperOpt et 3-opt permettant de bénéficier des avantages des deux approches, utilisant cette hybridation à l’intérieur d’une recherche à voisinage variable. Ils sont capables alors d’outrepasser les optima locaux et ainsi de créer des parcours de qualité.

Dynasearch [ Congram2000] est un autre exemple où des voisinages de grande taille sont explorés. Le voisinage où la recherche est exécutée se compose de toutes les combinaisons possibles, des étapes mutuellement indépendantes, d’une recherche simple . Un mouvement de Dynasearch se compose d’un ensemble de mouvements indépendants exécutés en parallèle par itération de recherche locale.

L’indépendance pour Dynasearch signifie que les différents mouvements n’interfèrent pas entre eux ; dans ce cas, la programmation dynamique peut être employée pour trouver la meilleure combinaison de mouvements indépendants. Dynasearch est limité aux problèmes où les étapes de recherche sont indépendantes, et n’a été jusqu’ici uniquement appliqué qu’aux problèmes où les solutions sont représentées par des permutations.

[ Puchinger et al. 2004] propose une combinaison AG/B&B pour résoudre le glass cutting problem où l’AG utilise une représentation sous forme de permutation : order-based laquelle est décodée par une heuristique gloutonne. L’algorithme de B&B est appliqué avec une certaine probabilité améliorant la phase de décodage en générant des sous-motifs optimaux.

N. Jussien et O. Lhomme [ Jussien and Lhomme2002] proposent un algorithme hybridant recherche locale et méthodes complètes. L’idée centrale de decision repair est basée sur des contraintes d’énumération, une affectation partielle est alors crée par ces contraintes, des contraintes d’énumération sont ensuite ajoutées. La recherche locale se réalise dans ce contexte sur un chemin de décision aidée par des techniques de filtrage. De plus une liste taboue des décisions est maintenue pour mémoriser les échecs rencontrés et guider la recherche.

Recouper les solutions

Les sous-espaces définis par le recoupement d’attributs depuis deux solutions ou plus, peuvent, comme le voisinage d’une seule solution, être aussi explorés par une méthode exacte.

Les algorithmes de [ Applegate et al. 1998, Klau et al. 2004] suivent cette idée, mais de manière séquentielle. Dans cette partie, nous nous focalisons sur un recoupement appliqué itérativement au travers d’une métaheuristique.

Dans le cadre [ Cotta and Troya2003] pour l’hybridation B&B et des algorithmes évolutionnaires, le B&B est utilisé en tant qu’opérateur d’un algorithme évolutionnaire. Les auteurs rappellent les concepts théoriques et notamment le potentiel dynastique de deux chromosomes x et y, correspondant à l’ensemble des individus porteurs d’information sur x et y. Basée sur ce concept, ils développent l’idée d’une recombinaison dynastique optimale.

Le résultat est un opérateur explorant le potentiel des solutions recombinées grâce au B&B, fournissant ainsi les meilleures combinaisons à partir des parents.

L’ensemble des expérimentations, comparant différents opérateurs de croisement avec cette méthode hybride, montre l’utilité d’une telle approche.

[ Marino et al. 1999] présente une approche où un AG est combiné à une méthode exacte pour le Linear Assignment Problem (LAP) afin de résoudre le problème de coloriage de graphes. L’algorithme LAP est incorporé dans l’opérateur de croisement et génère la permutation de couleurs optimale. Cet algorithme n’est pas plus performant que les autres approches, mais fournit des résultats comparables.

Filtrer l’espace de recherche

Si les métaheuristiques utilisent les contraintes pour une fonction d’évaluation, elles peuvent utiliser la formulation de ces contraintes et exploiter le fait qu’elles puissent réduire l’espace de recherche, notamment grâce aux algorithmes établissant la consistance. Dans [ Vasquez and Dupont2002], les contraintes binaires permettent un filtrage par arc consistance réduisant l’espace à explorer pour la méthode Tabou.

Utiliser le schéma d’une méthode incomplète pour une méthode complète

H. Deleau propose dans sa thèse [ Deleau2005] un cadre d’hybridation dans lequel la structure des algorithmes génétiques est utilisée pour modéliser un recherche complète. Le principe général des algorithmes génétiques est alors conservé, mais l’originalité vient du fait que cette fois les individus correspondent à des sous-ensembles de l’espace de recherche. Ce cadre unificateur intègre alors des mécanismes de réduction propres aux méthodes complètes sur ces individus pour réduire l’espace de recherche.

4.4 Conclusion

De telles combinaisons ont été aussi étudiées afin d’améliorer l’efficacité des méthodes évolutionnistes pour des CSP [ Tam and Stuckey1999, Riff Rojas1996]. Ces algorithmes hybrides sont appliqués aux divers problèmes de satisfaction de contraintes (satisfiabilité en logique propositionnelle [ Lardeux et al. 2005], le problème du voyageur de commerce...).

La principale conclusion que nous pouvons tirer est qu’il existe beaucoup d’opportunités pour développer de tels algorithmes hybridant méthodes exactes et techniques de recherche locale. Un certain nombre d’approches a été présenté, parfois complexes, pouvant être améliorées et étendues vers des applications différentes de celles proposées initialement.

Ces techniques partagent néanmoins une philosophie commune sur la combinaison de méthodes complètes et incomplètes. Une méthode est désignée comme le processus de recherche principal et une autre secondaire est utilisée comme heuristique d’amélioration avec une organisation hiérarchique est presque figée. Pour chaque méthode de résolution, une structure spécifique est décrite, ce qui limite les possibilités de se comparer aux autres méthodes.

Il est nécessaire dès lors, d’homogénéiser les définitions et les concepts mis en jeux pour la combinaison des méthodes complètes et incomplètes. Pour atteindre cette généralisation, la difficulté réside dans la recherche d’un cadre général unificateur.

Chapitre 5

Cadre et algorithme

générique pour la propagation

de contrainte

Krzysztof Apt présente dans [ Apt1997, Apt1999] un cadre théorique pour modéliser les opérations élémentaires effectuées par un solveur complet. Dans ce contexte, la propagation de contrainte et le filtrage correspondent au calcul du point fixe d’un ensemble de fonctions sur un ordre partiel. Ces fonctions, appelées fonctions de réduction, abstraient la notion de contraintes. Dans ce chapitre nous rappellerons le cadre et l’Algorithme Générique qui nous permet d’atteindre ce point fixe. Nous nous placerons dans le contexte des domaines composés pour approcher au mieux le modèle CSP.

5.1 Introduction

Comme le montrent les chapitres qui précèdent, il existe une grande variété de méthodes pour résoudre les problèmes de satisfaction de contraintes. Certaines utilisent la propagation de contraintes pour réduire les domaines et donc diminuer l’espace de recherche jusqu’à réduire éventuellement les domaines à de simples singletons. Dans ce chapitre nous allons présenter un cadre pour modéliser la propagation de contraintes, ses propriétés, et un algorithme générique issu de [ Apt2003]. Ce cadre nous sera très utile par la suite. En effet, il permet d’abstraire le fonctionnement des algorithmes pour la résolution des CSP. Cette abstraction consiste en une formulation mathématique des opérations de résolution et de leurs propriétés.

L’objectif est alors de montrer que la propagation de contraintes peut être expliquée en terme d’itérations chaotiques menant à un point fixe d’un ensemble fini de fonctions. Le calcul des limites d’ensembles de fonctions doit son origine à l’analyse numérique avec [ Chazan and Miranker1969], et fut adapté pour l’informatique avec [ Cousot1978, Cousot and Cousot1977]. Quant à l’idée de concevoir l’utilisation des contraintes en terme de fonctions, elle fut développée notamment par [ Benhamou1996] avec les fonctions de narrowing attachées aux contraintes, dans le contexte de l’arithmétique des intervalles réels. Le modèle des itérations chaotiques a aussi servi de cadre à [ Fages et al. 1998] pour des CSP dynamiques, dans les preuves de terminaisons d’exécutions d’opérateurs.

Dans un premier temps, nous présenterons le contexte, ou plutôt ce qui servira de support mathématique à la résolution et ses liens avec le modèle CSP traditionnel. Puis, nous verrons comment un algorithme générique peut s’écrire dans cette structure. Nous finirons en présentant les finalités de ce cadre, à savoir des propriétés de convergence.

5.2 Ordre partiel

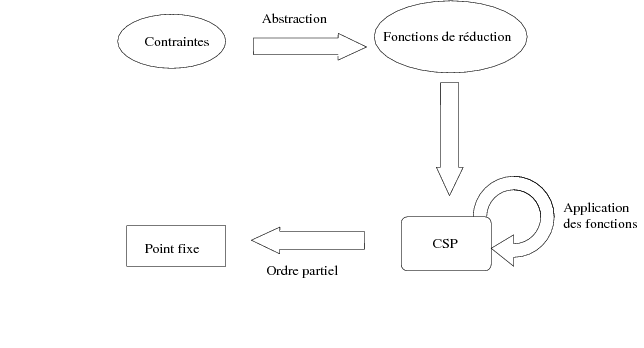
L’objectif du cadre défini par Apt, se servant de la notion d’ordre partiel, est de définir un ensemble de fonctions capables de converger vers un point fixe. En effet, la recherche des solutions, le processus de résolution est englobé dans une structure ordonnée.

La figure 5.1 schématise le cadre de résolution, nous y retrouvons les contraintes, celles-ci sont décrites sous forme d’opérateurs de réduction (fonctions de réduction). Les fonctions sont appliquées sur le problème modélisé en CSP et l’application de ces fonctions correspond en réalité à une succession de réductions dans un ordre partiel.

Figure 5.1: Modèle abstrait

Pour rappeler ce cadre les définitions suivantes sont nécessaires.

Définition 15 On dit d’une relation binaire R sur un ensemble D qu’elle est :

réflexive si (x,x) ∈ R pour tous x de D,

irréflexive si (x,x) ∉ R pout tous x de D,

antisymétrique si quelques soient x,y ∈ D on a (x,y) ∈ R et (y,x) ∈ R alors x=y,

transitive si pour tous x,y,z ∈ D on (x,y) ∈ R et (y,z) R alors on a aussi (x,z) ∈ R.

Ainsi par ordre partiel nous entendons un couple (D,\sqsubseteq) formé à partir d’un ensemble D et d’une relation réflexive, antisymétrique et transitive notée \sqsubseteq qui porte sur D. Un élément e de D est appelé plus petit élément si ∀d ∈ D on a e \sqsubseteq d.

5.3 Fonctions et propriétés

L’ordre partiel constitue ici le support de calcul pour les fonctions que nous utiliserons. Mais pour obtenir un point fixe, et afin d’établir une certaine cohérence dans les mécanismes en jeu, des propriétés fondamentales sur ces fonctions sont nécessaires.

Définition 16 Soit un ordre partiel (D,\sqsubseteq) et une fonction f sur D.

f est dite inflationnaire si x \sqsubseteq f(x) pour tout x.

f est dite monotone si x \sqsubseteq y implique que f(x) \sqsubseteq f(y) pour tous x,y.

Définition 17
Soit un ensemble D, un élément d ∈ D et un ensemble de fonctions F = { f₁,...,f_k} portant sur D.

une exécution (de fonctions f₁,...,f_k) correspond à une séquence infinie de nombre de [1..k].

une exécution i₁,i₂,... est dite équitable si tout i ∈ [1..k] apparaît une infinité de fois.

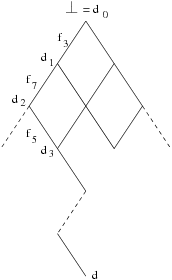
Cette dernière notion d’équité trouve son importance, comme le précise K. Apt, dans l’étude de la propagation de contrainte où lorsque pour la première fois sont introduites dans [ Gusgen and Hertzberg1988] les itérations chaotiques de fonctions de réduction monotones.

Nous avons présenté la structure et les fonctions. Regardons maintenant à quoi correspond l’application de ces fonctions. La notion d’ordre partiel sert de support mathématique aux calculs, aux itérations des fonctions. Considérons un ordre partiel (D,\sqsubseteq) avec son plus petit élément ⊥ et un ensemble fini de fonctions F={f₁,...,f_k} sur D.

Une itération de F est définie comme une de valeurs d₀,d₁,d₂...induite par : d₀ = ⊥.
d_j = f_{i_j}(d_j-1). avec i_j ∈ [1..k].
On a une suite croissante d₀ \sqsubseteq d₁ \sqsubseteq d₂ ... d’éléments de D qui peut se stabiliser en d si pour j ≥ 0 on a d_i = d pour i ≥ j.

Figure 5.2: Exemple d’ordre partiel

Exemple : Ordre partiel La figure 5.2 schématise un ordre partiel dans lequel un élément initial d₀ est transformé en un élément d₁ par une fonction f₃ et ainsi de suite : d₁ = f_3₁(d₀), d₂ = f_7₂(d₁), d₃ = f_5₃(d₂).

Rappelons que l’objectif de ce modèle est de décrire le comportement des algorithmes de propagation. Revenons donc sur les notions de consistances qui sont la base de la résolution. Les algorithmes associés aux consistances ont pour but de supprimer les valeurs des domaines, de les réduire, dans notre contexte elles seront modélisées par des fonction de réduction.

Définition 18 [Fonctions de réduction] Soit une séquence de domaines D₁, D₂, ..., D_n associé à leurs ensembles des parties P(D_i) pour i ∈ [1..n], soit D les produits cartésiens des P(D_i), et soit d un élément de D. Une fonction de réduction est une fonction telle que :

d \sqsubseteq f(d)

Lemme : Stabilisation. Considérons l’ordre partiel (D,\sqsubseteq) avec un plus petit élément que l’on note ⊥ et un ensemble fini de fonction monotones F portant sur D. Supposons qu’une itération de F se stabilise en un point fixe d. Alors d est le plus petit point fixe commun des fonctions de F.

: Soit d₀, d₁,... l’itération en mentionnée. Pour un certain j ≥ 0 on a d_i = d pour i ≥ j. Considérons un point fixe e des fonctions de F. Nous pouvons prouver que d \sqsubseteq e. La preuve se fait par induction sur i avec d_i \sqsubseteq e. La proposition est vraie pour i=0 puisque d₀ = ⊥. Supposons maintenant que cela est vrai pour i ≥ 0. Nous avons d_i+1 = f_j(d_i) pour un j ∈ [1..k]. De part la monotonie de la fonction f_j et de l’hypothèse d’induction f_j(d_i) \sqsubseteq f_j(e), on a d_i+1 \sqsubseteq e car par définition f_j(e) = e.

^[¯]

5.4 Application aux CSP et domaines composés

Nous pouvons à présent nous rapprocher du modèle CSP et de sa résolution. L’ordre partiel est alors instancié par les domaines du CSP où les différents CSP obtenus lors de la résolution par propagation sont des éléments de l’ensemble D. Pour être plus formel, il nous faut décrire l’ensemble des CSP que l’on peut obtenir à partir du CSP initial.

Soit un CSP (X, D, C), on appelle l’ensemble des parties de D, noté P(D), l’ensemble des sous-ensembles possibles de D. On obtient un ordre partiel, si nous considérons l’ordre (P( D), ⊇ ), où ⊇ est la relation d’inclusion inverse ensembliste.

Un CSP ne se limite pas à un domaine, il nous faut alors considérer l’ensemble des domaines des variables et donc le produit cartésien de ces domaines.

Soit le produit cartésien P(D₁) ×... × P(D_n) dont les éléments sont ordonnés de la façon suivante :

(X₁,...,X_n) ⊇ (Y₁, ..., Y_n) ssi ∀i ∈ [1..n] X_i ⊇ Y_i

Le couple (P(D₁) ×... × P(D_n), ⊇ ) forme un ordre partiel.

Dans le formalisme introduit par Apt, à son niveau d’abstraction le plus élevé, une étape de résolution de CSP est considérée comme un élément, et toute opération, pour passer à une étape suivante, est modélisée par une simple fonction. Une analogie est alors faite, entre la résolution et le chemin dans un ordre partiel spécifique.

Exemple : Fonctions de réduction Reprenons notre exemple 2.2 dans lequel un CSP ne contient que la contrainte c : x < y avec D_x = [5..10] et D_y = [3..7]. Nous pouvons alors considérer deux fonctions de réduction de D → D :

Arc_consistence1 : (D_x,D_y) → (D_x’,D_y) t.q. D_x’ = {a ∈ D_x | ∃b ∈ D_y, a < b}
Arc_consistence2 : (D_x,D_y) → (D_x,D_y’) t.q. D_y’ = {b ∈ D_y | ∃a ∈ D_x, a < b}

Ces principes étant définis nous pouvons énoncer un algorithme générique dont beaucoup d’algorithmes de propagation de contraintes présents dans la littérature sont des instances.

L’objectif est alors d’obtenir un point fixe de l’ensemble des fonctions.

5.5 Algorithme générique itératif

Le calcul du plus petit point fixe commun d’un ensemble de fonctions F est obtenu par l’algorithme suivant :

[!hbt]

#1GI: Algorithme Générique Itératif

où G est l’ensemble courant des fonctions restant à appliquer (G ⊆ F), d est un ensemble partiellement ordonné et, pour tout G,g,d, l’ensemble des fonctions actualise(G,g,d) de F est tel que :

A : { f ∈ F - G | f(d) = d ∧f(g(d)) ≠ g(d)} ⊆ actualise(G,g,d).
B : g(d) = d implique que actualise(G,g,d) = Æ.
C : g(g(d)) ≠ g(d) implique que g ∈ actualise(G,g,d)

Supposons que toutes les fonctions de F soient croissantes, (x\sqsubseteq f(x) pour tout x) et monotones (x \sqsubseteq y implique f(x) \sqsubseteq f(y) pour tout x,y) et que (D,\sqsubseteq) est fini. Alors, chaque exécution de l’algorithme GI termine et calcul d, le plus petit point fixe commun des fonctions de F(voir [ Apt1997]). Notons que pour ce qui suit, nous considérons seulement des ordres partiels finis.

La propagation de contraintes se matérialise par l’instanciation de l’algorithme GI:

L’ordre \sqsubseteq est instancié par ⊇ , l’inclusion ensembliste habituelle,
d : = ⊥ correspond à d : = D₁ ×...× D_n, le produit cartésien des domaines des variables du CSP,
F est un ensemble de fonctions de réduction monotones et croissantes qui abstraient les contraintes pour réduire les domaines des variables.

Le résultat obtenu est la plus petite boîte (i.e., produit cartésien des domaines) relativement aux fonctions de réduction de domaines, qui contient les solutions du CSP.

5.6 Conclusion

Nous avons introduit dans ce chapitre la propagation de contrainte comme une instance d’un algorithme itératif. D’une part, ceci simplifie le raisonnement autour de la validité des algorithmes et clarifie leurs natures. Plus précisément, ce modèle considère un algorithme générique itératif sur un ordre partiel dont l’exactitude devient une preuve. Les algorithmes instanciés en ordre partiel et en fonction de réduction offrent une voie, par cette généralité, vers une multitude de méthodes de propagation. D’autre part, ce cadre abstrait nous servira de base pour l’étendre vers une future hybridation avec des méthodes incomplètes telle la recherche locale et les algorithmes génétiques.

Part 2

Cadre théorique uniforme pour la

résolution des CSP

Chapitre 6

Introduction de la recherche

locale

L’objectif de ce chapitre est de proposer une extension du modèle décrit dans le chapitre 5, en considérant d’une part les méthodes complètes vues au chapitre 2 et d’autre part les méthodes incomplètes du chapitre 3. Dans ce chapitre, nous présenterons un cadre formel d’hybridation pour ces techniques ainsi que des expérimentations mettant en avant l’intérêt de ce cadre.

6.1 Introduction

Dans le chapitre 5, nous avons présenté un modèle qui repose sur les itérations chaotiques pour définir un cadre mathématique d’itération d’un ensemble fini de fonctions sur des domaines abstraits munis d’un ordre partiel. Ce cadre est particulièrement adapté à la résolution de CSP par propagation de contraintes : les domaines sont instanciés par les domaines de valeurs des variables et les fonctions par des fonctions de réduction de domaines qui éliminent les valeurs inconsistantes (relativement aux contraintes) de ces domaines.

Afin d’obtenir un solveur complet (i.e., un solveur capable de décider un CSP admet ou non des solutions), la propagation de contraintes est associée à un mécanisme de découpage des domaines (tel que l’énumération) afin de diviser l’espace de recherche en zones plus petites au sein desquelles on peut espérer continuer la propagation. La propagation et la découpe alternent alors jusqu’à ce qu’une solution soit obtenue.

Dans ce chapitre, nous proposons un modèle étendu pour l’hybridation intégrant le découpage et la recherche locale par le biais de 3 notions : les échantillons qui sont des points représentatifs de l’espace de recherche, un voisinage qui détermine comment se déplacer d’un échantillon vers un autre et une fonction d’évaluation qui permet d’estimer la qualité des échantillons. La recherche locale explore alors l’espace de recherche en se déplaçant d’échantillon en échantillon afin d’atteindre un optimum. Ces mouvements sont modélisés dans ce cadre comme des fonctions de réduction.

Nous introduisons dans notre modèle la notion de SCSP, i.e., des CSP intégrant des échantillons. Nous intégrons également la découpe comme un ensemble de fonctions de réduction. Ainsi, les domaines abstraits des itérations chaotiques sont instanciés par une union (ensemble) de SCSP. Les fonctions de réduction de domaines habituelles (propagation de contraintes) sont étendues pour s’intégrer à ce cadre. De nouvelles fonctions (les fonctions de recherche locale) sont introduites pour se déplacer d’échantillon en échantillon : ces fonctions ont alors les bonnes propriétés pour être utilisées dans l’algorithme des itérations chaotiques.

Dans ce cadre, la propagation de contraintes, les mouvements de recherche locale et les fonctions de découpe sont considérés au même niveau et appliqués aux SCSP. Comme l’ordre d’application de ces fonctions est libre, ce cadre nous permet d’envisager diverses stratégies de combinaison. De plus, le calcul correspond encore à l’obtention d’un point fixe.

Afin d’illustrer notre modèle, nous présentons des expérimentations réalisées avec un solveur hybride permettant d’évaluer les bénéfices et avantages liés à une résolution mixte. Les caractéristiques des combinaisons étudiées peuvent alors être clairement spécifiées dans notre modèle.

6.2 Échantillons et voisinage

Pour unifier les structures de données des différentes méthodes, nous allons définir la notion d’échantillon que manipule la recherche locale ainsi que la notion de voisinage.

6.2.1 Échantillonnage et Notion de solution

La réduction de domaine et le découpage agissent sur les domaines des variables, tandis que la recherche locale opère sur une structure différente correspondant en général à un ensemble particulier de valeurs (points) des domaines. Nous proposons ici une définition plus générale et abstraite de la recherche locale, fondée sur la notion d’échantillon.

Définition 19 [Échantillon] Étant donné un CSP (X,D,C), nous définissons une fonction d’échantillonnage ε: D → P(D). Par extension, ε(D) désigne l’ensemble U_{d ∈ D} ε(d).
Généralement, ε(d) est réduit à d et ε(D)=D, c’est-à-dire que la recherche locale manipule directement les affectations, mais cela peut également être un agrégat de points autour de d, ou une boîte de n-uplets couvrant d (e.g., pour les domaines continus). De même, aucune condition n’impose que d ∈ varepsilon(d).

De plus, il apparaît comme essentiel que ε(D) contienne toutes les solutions. En effet, l’espace de recherche D est abstrait par ε(D) pour être utilisé par la recherche locale et doit donc être capable d’en isoler les solutions.

Dans ce contexte, la recherche locale repose sur une fonction de voisinage sur ε(D) et sur l’ensemble des échantillons déjà visités dans un chemin, elle est alors décrite par :

Une fonction de voisinage sur ε(D), qui calcule l’ensemble des échantillons voisins pour chaque échantillon de ε(D);
et un ensemble de chemins de recherche locale. Chaque chemin étant composé de la suite des échantillons visités et représente le passage de voisin en voisin.

Le principe fondamental de la recherche locale est son exploration basée sur la notion de voisinage.

Définition 20 Nous définissons, en utilisant la notion d’échantillonnage, une fonction de voisinage par :

N :ε(D) → P(ε(D))

La recherche se fait par déplacement de proche en proche à l’aide de la fonction de voisinage, ce qui forme un chemin dans l’espace de recherche et l’ensemble des chemins de recherche locale possibles est défini par LS_D=

∪
i > 0
{p=(s₁,...,s_i) ∈ ε(D)ⁱ | ∀j, 1 ≤ j < i-1, s_j+1 ∈ N(s_j) et s₁ ∈ ε(D)}

D’un point de vue pratique, une recherche est limitée par un chemin fini par rapport à un critère d’arrêt : celui-ci peut correspondre à un nombre maximum d’itérations (i.e. longueur du chemin) ou dans le contexte de la résolution de CSP, au fait qu’une solution soit atteinte.

Définition 21
Comme nous avons vu au chapitre 3, la fonction d’évaluation guide la recherche, dans notre contexte, nous considérons la fonction

eval :ε(D) →ℵ

telle que eval(s) représente le nombre de contraintes non-satisfaites par l’échantillon s. De plus, nous imposons que eval(s) soit égale à 0 si et seulement si s est solution du problème. Nous notons s < _eval s’ le fait que eval(s) < eval(s’).
Rappelons que notre objectif est d’être capable de réunir en un même modèle les caractéristiques de méthodes de natures différentes. L’utilisation du cadre des itérations chaotiques impose la définition d’une structure ordonnée. Avec cette formulation de la recherche locale, nous allons pouvoir définir un premier ordre. Cette relation d’ordre nous permet, par la suite, une intégration avec les méthodes à base de propagation de contraintes.

6.2.2 Ordre sur les échantillons

D’un point de vue pratique, pour la recherche locale, un résultat est soit un chemin menant à une solution, soit un chemin d’une taille maximale donnée. Nous définissons alors un ordre, qui par sa définition, nous permettra une meilleure intégration de la recherche locale dans le modèle décrit au chapitre 5.1. L’idée est de formuler l’avancement de la recherche comme une progression dans une structure ordonnée. Pour ce faire, nous allons donc concevoir un ordre sur les chemins de recherche locale, de sorte qu’un chemin sera dit plus grand s’il correspond à une avancée en terme de recherche. Cela se traduit comme une amélioration ou un dernier échantillon meilleur d’après la fonction d’évaluation. De même, étant donné que nous décrivons l’évolution de la recherche, les plus grands éléments dans cet ordre sont les chemins menant à une solution ou les chemins de taille maximale. Pour être en accord avec ces principes, nous définissons un ordre sur la recherche locale comme suit :

Définition 22 [Relation d’ordre pour la recherche locale]

Considérons une relation \sqsubseteq_ls sur LS_D définie par:

(s₁,..., s_n) \sqsubseteq_ls (s₁,..., s_n)

(s’₁, ..., s’_m) \sqsubseteq_ls (s₁, ..., s_n) si n > m et ∀j, 1 ≤ j ≤ m,eval(s’_j) ≠ 0
et ∀i, 1 ≤ i ≤ n, eval(s_i) ≠ 0

(s’₁, ..., s’_m) \sqsubseteq_ls (s₁, ..., s_n) si eval(s_n)=0, ∀i, 1 ≤ i ≤ n-1, eval(s_i) ≠ 0
et ∀j, 1 ≤ j ≤ m, eval(s’_j) ≠ 0

Cette relation nous sera utile pour comparer des chemins de recherche et donc par là, l’avancement d’une recherche locale.

Propriété 1 L’ensemble des chemins possibles LS_D muni de la relation \sqsubseteq_ls forme un ordre partiel.

Pour prouver l’un ordre partiel (LS_D, \sqsubseteq_ls), nous devons démontrer que :

la relation est réflexive;
la relation est transitive;
la relation est antisymétrique.

Le premier point est obtenu de manière directe depuis la définition de la relation.

Pour le second, étant donnés (r₁,..., r_m) \sqsubseteq_ls (s₁,..., s_n) et (s₁,..., s_n) \sqsubseteq_ls (t₁,..., t_q) montrons que (r₁,..., r_m) \sqsubseteq_ls (t₁,..., t_q). Tout d’abord si (r₁,..., r_m) = (s₁,..., s_n) ou si (s₁,..., s_n) = (t₁,..., t_q) la preuve est directe.

Supposons l’existence de solution parmi les trois chemins, il est clair que ni (r₁,..., r_m), ni (s₁,..., s_n) ne peuvent contenir de solution car tous deux admettent un élément qui leur est supérieur. Donc si solution il y a, on a (t₁,..., t_q) avec eval(t_q)=0. Or d’après la définition de l’ordre, l’existence de cette solution suppose que tout autre chemin ne contenant pas de solution lui est inférieur donc (r₁,..., r_m) \sqsubseteq_ls (t₁,..., t_q).

Enfin pour terminer la preuve de la transitivité, nous allons considérer la longueur des chemins. Nous déduisons de la définition de la relation que les chemins de tailles identiques, ne contenant pas de solution, ne sont pas comparables. Or si les chemins sont de longueurs différentes (m > n > q), alors m > q est donc (r₁,..., r_m) \sqsubseteq_ls (t₁,..., t_q).

Il nous faut maintenant prouver l’antisymétrie : si (r₁,...,r_m) \sqsubseteq_ls (s₁,..., s_n) et (s₁,..., s_n)\sqsubseteq_ls (r₁,..., r_m) alors (r₁,..., r_m) = (s₁,..., s_n). Nous ne pouvons avoir n ≠ m et de solution dans l’un des deux chemins donc si les chemins sont comparables dans les deux sens c’est qu’ils sont égaux et donc la relation est antisymétrique.

De la réflexivité, la transitivité et l’antisymétrie de la relation, nous en concluons que le couple (LS_D,\sqsubseteq_ls) forme un ordre partiel.

^[¯]

L’exemple 7 illustre la notion de résultats dans un processus de recherche locale.

Exemple : Chemin LS
Considérons p₁=(a,b), p₂=(a,c) et p₃=(b) trois éléments de LS_D tels que eval(b)=0 (i.e., b est solution). Alors, ces trois chemins correspondent à des résultats possibles d’une recherche locale de taille 2, ils ne sont pas comparables vis-à-vis de la définition 22.

Grâce à cet ordre pour la recherche locale, nous allons pouvoir créer notre cadre d’hybridation. En effet, nous allons intégrer cette notion de chemin d’échantillons dans le modèle CSP.

6.3 Modèle de calcul

Nous pouvons dès à présent définir la structure requise pour une hybridation de la recherche locale et de la propagation de contraintes. Pour arriver à nos fins, nous allons passer par une instanciation du cadre abstrait décrit par K. Apt et présenté au chapitre 5.

Définition 23 [CSP échantillonné] Un CSP échantillonné (sCSP) est défini par un triplet (D,C,p), une fonction d’échantillonnage ε, et un chemin de recherche locale p où

D = D₁×... ×D_n

∀c ∈ C, c ⊆ D₁ ×... ×D_n

p ∈ LS_D

Notons que, dans notre définition, le chemin de recherche locale p se doit d’être inclus dans la boîte définie par ε(D). Ainsi une modification apportée sur D aura des conséquences directement sur ε(D) et donc sur la recherche locale. Ce que nous voulons avant tout c’est faire coexister les méthodes pour que les bénéfices apportés par l’une se répercutent sur l’autre. Le fait d’imposer un échantillonnage sur D permet de synchroniser les modifications opérées sur les domaines avec les points de recherche locale qui restent alors dans l’espace de recherche courant du problème. On note SCSP l’ensemble des sCSP. Nous pouvons maintenant définir la relation d’ordre sur la structure échantillonnée (SCSP,\sqsubseteq) pour nous rapprocher du modèle décrit par Apt.

Définition 24 [Relation d’ordre sur les CSP échantillonnés]
Étant donné deux sCSP
y = (D,C,p) et y’=(D’,C,p’),

y\sqsubseteq y’ ssi D’ ⊂ D ou (D’ = D et p \sqsubseteq_ls p’).

Le couple (SCSP,\sqsubseteq) forme un ordre partiel, car du point de vue de l’inclusion ensembliste nous avons un ordre partiel et la définition précise qu’en cas d’égalité des ensembles nous nous retrouvons dans le contexte de l’ordre sur les chemins de recherche, lui-même prouvé comme partiel.
Cette relation est étendue sur P(SCSP), car nous verrons par la suite, que la résolution se fait sur un ensemble de SCSP :

{f₁,...,f_k} \sqsubseteq {y₁,...,y_l} ssi ∀f_i, (∃y_j, f_i\sqsubseteq y_j et \not ∃y_j, y_j\sqsubset f_i)

où i ∈ [1..k],j ∈ [1..l].

Propriété 2 L’ensemble P(SCSP) muni de la relation \sqsubseteq forme un ordre partiel.

Pour prouver l’un ordre partiel, nous devons démontrer que :

la relation est réflexive;
la relation est transitive;
la relation est antisymétrique.

La réflexivité de la relation est directe car elle n’est pas définie comme stricte. La transitivité se déduit aussi de la définition donnée de la relation avec :

{f₁,...,f_k} \sqsubseteq {y₁,...,y_l}

{y₁,...,y_l} \sqsubseteq {p₁,...,p_m}

Montrons que

{f₁,...,f_k} \sqsubseteq {p₁,...,p_m}

D’après la définition on a :

∀f_i, (∃y_j, f_i \sqsubseteq y_j et \not ∃y_j, y_j \sqsubset f_i)

où i ∈ [1..k],j ∈ [1..l] et

∀y_j, (∃p_t, y_j \sqsubseteq p_t et \not ∃p_t, p_t \sqsubset y_j)

où j ∈ [1..l],t ∈ [1..m]
Nous en déduisons que :

∀f_i, (∃p_t, f_i \sqsubseteq p_t et \not ∃p_t, p_t \sqsubset f_i)

où i ∈ [1..k],t ∈ [1..m]
La relation est donc bien transitive.

Considérons maintenant l’antisymétrie de la relation :

Hypothèse 1 :

{f₁,...,f_n} \sqsubseteq {y₁,...,y_m} ssi ∀f_i, (∃y_j, f_i\sqsubseteq y_j et \not ∃y_j, y_j\sqsubset f_i)

où i ∈ [1..n],j ∈ [1..m].

Hypothèse 2 :

{y₁,...,y_m} \sqsubseteq {f₁,...,f_n} ssi ∀y_j, (∃f_i, y_j\sqsubseteq f_i et \not ∃f_i, f_i\sqsubset y_i)

où i ∈ [1..n],j ∈ [1..l]

Si nous réunissons les propriétés qui découlent de la définition nous obtenons ceci :

∀f_i, (∃y_j, f_i \sqsubseteq y_j et \not ∃y_j, y_j \sqsubset f_i)

∀y_j, (∃f_i, y_j \sqsubseteq f_i et \not ∃f_i, f_i \sqsubset y_i)

Or si nous croisons ces informations, c’est à dire que nous prenons la partie à gauche du et de l’hypothèse 1 avec la partie droite de l’hypothèse 2, nous obtenons que :

∀f_i, (∃y_j, f_i \sqsubseteq y_j) et ∀y_j (\not ∃f_i, f_i\sqsubset y_i)

et donc que :

∀f_i, (∃y_j, f_i = y_j)

si nous faisons de même avec l’autre croisement :

∀y_j, (∃f_i, y_j \sqsubseteq f_i) et ∀f_i (\not ∃y_j, y_j\sqsubset f_i)

donc

∀y_j, (∃f_i, y_j = f_i)

∀f_i, (∃y_j, f_i = y_j)

Nous pouvons alors en conclure que :

{f₁,...,f_n} = {y₁,...,y_m}

et que la relation est antisymétrique, transitive et réflexive.

^[¯]

Notons SCSP l’ensemble P(SCSP) qui constitue l’ensemble clef de la structure de calcul. Un élément de cet ensemble SCSP est noté sCSP. Un sCSP est ainsi un ensemble de sCSP. Comme dans [ Apt1997], nous désignons par ⊥ le plus petit élément {(D,C,p)} (i.e., le sCSP initial à résoudre).

6.4 Les solutions

Comme notre cadre est dédié à la résolution de CSP, nous nous devons de fournir une description précise de la notion de solution en accord avec la structure mentionnée précédemment. Ces notions sont clairement définies de part et d’autre pour les méthodes complètes et incomplètes.

Du point de vue d’une résolution complète, une solution d’un CSP est un n-uplet de l’espace de recherche satisfaisant toutes les contraintes. Pour ce qui est de la recherche locale, la notion de solution est étroitement liée à la fonction eval, qui désigne comme solution un élément s de ε(D) tel que eval(s) = 0.

Définition 25 [Solutions]

Étant donné un sCSP y = (D,C,p), l’ensemble des solutions de y est défini par :

pour les solveurs à base de propagation de contraintes(CP):

Sol_D(y) = { d ∈ D | ∀c ∈ C, d ∈ c }

pour la recherche locale (LS):

Sol_{LS_D}(y)={(s₁,...,s_n) ∈ LS_D | eval(s_n)=0}

pour un solveur hybride LS/CP :

Sol(y) = {(d,C,p)| d ∈ Sol_D(y) ou p ∈ Sol_{LS_D}(y)}

Cette notion est étendue pour chaque sCSP Y par :

Sol(Y) =
∪
y ∈ Y
Sol(y)

Nous avons présenté le modèle de calcul ainsi que la notion de solution, il nous reste maintenant à présenter comment nous allons utiliser cette structure, quelles sont les transformations du problème initial pouvant nous mener aux solutions. La figure 6.1 illustre l’ordre pour l’hybridation et donne l’intuition du processus de recherche par l’application de fonctions.

Figure 6.1: Processus hybride de résolution sur un ordre partiel

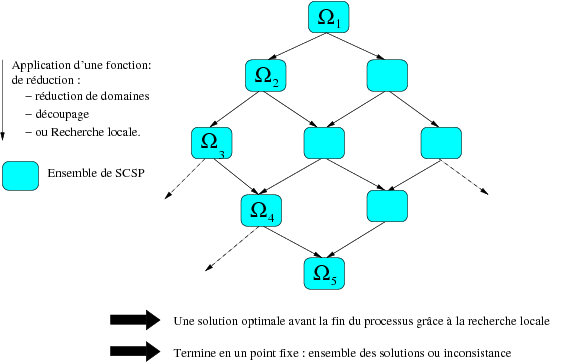
6.5 Fonctions de réduction : définition et propriétés

La structure SCSP a été définie pour une intégration de CP et LS, nous devons dès lors définir nos fonctions hybrides qui seront ensuite utilisées par l’algorithme GI. En effet, que ce soit les déplacements de la recherche locale ou l’utilisation des contraintes pour réduire l’espace de recherche, toutes ces opérations seront assimilées à des fonctions de réduction.

Soit un sCSP Y = {y₁,...,y_n} de SCSP, il nous est nécessaire de définir les fonctions sur Y correspondant à la réduction de domaines, au découpage et à la recherche locale, car chaque catégorie de fonction que nous allons appliquer sur un sCSP a ses propriétés bien distinctes. De plus, les fonctions peuvent s’appliquer sur plusieurs sCSP y_i de Y, et pour chaque y_i sur ses différents composants. En raison du fait qu’ici nous considérons des CSP avec des domaines finis, notre structure est un ordre partiel fini.

Nous allons donc commencer par présenter de quelle manière la réduction de domaine est définie telle des fonctions de réduction puis l’énumération par découpage des domaines et enfin les fonctions correspondant à la recherche locale.

6.5.1 Réduction de domaines

Réduire les domaines signifie retirer des domaines des variables, des valeurs ne pouvant appartenir à une solution. Cette réduction de domaine est la conséquence de l’utilisation des contraintes, dont l’objectif est d’atteindre la propriété de consistance comme présentée au chapitre 2.3. Les fonctions de réduction (voir chapitre 5) abstraient donc l’utilisation des contraintes pour réduire ainsi l’espace de recherche et sont étendues ici au SCSP.

Définition 26 [Fonction de réduction de domaines]
Une fonction de réduction de domaines red est une fonction :

red :SCSP → SCSP

{y₁, ..., y_n} → {y’₁,..., y’_n}

telle que ∀i ∈ [1...n ]:

soit y_i = y’_i

ou soit y_i = (D,C,p), y’_i = (D’,C,p’) et D ⊇ D’ et Sol_D(y_i) = Sol_D(y’_i).

Notons que cette définition garantit que {y₁, ...,y_n} \sqsubseteq red({y₁, ..., y_n}) et que cette fonction est inflationnaire et monotone sur (SCSP,\sqsubseteq). De plus, cette définition impose que p’ ∈ LS_D’ et permet de décrire une fonction qui réduit plusieurs domaines issus de différents sCSPs d’un sCSP en même temps. Du point de vue de la programmation par contraintes, une fonction de réduction préserve l’ensemble des solutions du CSP initial : aucune solution n’est perdue par une fonction de réduction de domaines car, les valeurs supprimées sont considérées comme inconsistantes vis-à-vis des contraintes et donc ne peuvent appartenir à une quelconque solution du problème. Cette nécessité de conserver les valeurs des domaines qui peuvent être solution est aussi présente lors d’un découpage des domaines.

6.5.2 Découpage de domaines

La réduction des domaines à elle seule ne garantit pas l’obtention d’une solution. En effet le découpage, pouvant aller jusqu’à l’énumération, est nécessaire pour obtenir une affectation complète (une seule valeur par domaine) comme nous l’avons vu au chapitre 2.4. L’idée est donc de diviser le problème en deux (voire plus) et de résoudre les sous problèmes indépendamment. Le découpage se fait en général sur une variable dont on découpe le domaine.

Définition 27 [Découpage de domaines]
Une fonction de découpage de domaines est une fonction sp sur SCSP telle que pour tout Y = {y₁,..., y_n} ∈ SCSP:

a. sp(Y)={y’₁, ..., y’_m} avec n ≤ m,
b. ∀i ∈ [1..n],

soit ∃j ∈ [1..m] tel que y_i = y’_j

ou soit il existe y’_j₁, ..., y’_{j_h}, j₁, ..., j_h ∈ [1..m] tels que

Sol_D(y_i) =
∪
k=1..h
Sol_D(y’_{j_k})

c. et, ∀j ∈ [1..m],

soit ∃i ∈ [1..n] tel que y_i = y’_j

ou y’_j = (D’,C,p’) et il existe y_i = (D,C,p), i ∈ [1..n] tels que D É D’.

Les conditions a. et b. garantissent que des sCSP ont été découpés en sous-sCSP par découpage de leurs domaines (un ou plusieurs domaines de variables) en plus petits domaines sans écarter de solutions (défini par l’union des solutions de y_i). La condition c. garantit que l’espace de recherche n’augmente pas : chaque domaine des sCSP de Y’ est inclus dans l’un des domaines de sCSP composant Y. Notons que, les domaines de différentes variables de différents sCSP peuvent être découpés en même temps.

Les fonctions de réduction et les fonctions de découpage nous permettent une résolution complète, mais nous allons voir que nous pouvons aussi définir sur ce modèle des fonctions de recherche locale.

6.5.3 Le Recherche locale

Nous pouvons décrire le comportement de la recherche locale par l’application de fonctions, mais dans ce cas de figure la recherche ne se fait que sur la partie échantillonnage que nous avons définie plus tôt.

Définition 28 [La recherche locale]

Une fonction de recherche locale l_N est une fonction

l_N :SCSP → SCSP

{y₁, ..., y_n} → {y’₁,..., y’_n}

où

N est le nombre maximum de mouvements consécutifs

∀i ∈ [1..n]

soit y_i=y’_i

ou y_i=(D,C,p) et y_i’=(D,C,p’) avec p=(s₁,...,s_k) et p’=(s₁,...,s_k,s_k+1) tel que s_k+1 ∈ N(s_k) ∩D et k+1 ≤ N.

Le paramètre N représente la longueur maximale du chemin de recherche locale, i.e., le nombre de pas autorisés pour une recherche locale. Une fonction de recherche locale peut essayer d’améliorer l’échantillon d’un ou plusieurs sCSP en même temps. Même si l_N tente de réduire y_i, il se peut que y_i=y’_i survienne quand :

p ∈ Sol_{LS_D}(y): le dernier échantillon s_n du chemin de recherche locale courant ne peut être amélioré par l_N,
la longueur n du chemin de recherche est telle que n=N : le nombre maximum de mouvements autorisé est atteint,
l_N est la fonction identité sur y_i, i.e., l_N n’essaie plus d’améliorer le chemin de recherche locale du sCSP y_i. Ceci se produit si aucun mouvement ne peut s’effectuer (e.g., un algorithme de descente a atteint son minimum local ou tous les voisins sont tabous pour un algorithme de recherche tabou [ Glover and Laguna1997]).

Nous avons donc trois types distincts de fonctions : red, sp et l qui correspondent respectivement à la réduction de domaine, au découpage et à la recherche locale. Dans ce qui suit, nous allons présenter la résolution des sCSP et plus particulièrement l’organisation de l’application de ces fonctions.

6.6 La résolution d’un sCSP

Pour la résolution complète d’un sCSP {(D₁×...×D_n, C,p)} l’algorithme GI doit être instancié de la manière suivante :

[!hbt]

#1GI: Algorithme Générique Itératif instancié

L’ordre \sqsubseteq est instancié par l’ordre donné dans la définition 24,
d : = ⊥ correspond à d : = {(D₁×...×D_n, C,p)},
F est un ensemble de fonctions monotones inflationnaires données, comme définis en section 6.5 : fonction de réduction de domaines (extensions des fonctions de réduction de domaines de CSP habituelles), fonctions de découpage (mécanismes standards de découpage assimilés à des fonctions de réduction), et les fonctions de recherche locale (e.g., fonctions pour la descente, la recherche tabou, etc).

Nous proposons maintenant une instanciation du schéma de fonctions présenté. D’un point de vue opérationnel, les fonctions de réduction doivent être appliquées sur des sCSP sélectionnés dans un ensemble sCSP donné.

En pratique, nous construisons les fonctions sur des sCSP puis, nous étendons ces fonctions pour qu’elles s’appliquent sur l’ensemble sCSP. C’est ainsi qu’une fonction (de réduction, de découpage ou de recherche locale) sur sCSP sera conduite par un opérateur de sélection, pour déterminer sur quel sCSP de sCSP la fonction doit opérer.

6.6.1 Les fonctions de sélection

Comme le montre la figure 6.2, pour appliquer les fonctions de réduction, nous devons préalablement choisir : d’une part sur quel sCSP noté f_k de l’ensemble F la fonction agira, et d’autre part, nous devons sélectionner le domaine sur lequel cette fonction sera appliquée.

Picture Omitted

Picture Omitted
Figure 6.2: Fonction de sélection

Définissons ces opérateurs de sélection dans un cadre général. Soit une fonction de sélection :

select :A → P(B)

Considérons une fonction

f^select :A → C

telle que

f^select(x) = g(y), y ∈ select(x)

où

g :B → C

Par conséquent, f^select peut être vue comme une fonction non déterministe (i.e. une relation). Formellement, on associe à chaque fonction f^select une famille de fonctions déterministes (fⁱ)_{i > 0} telles que ∀x ∈ A, ∀y ∈ select(x), ∃k > 0, f^k(x)=g(y). Si on considère les ensembles A et B finis alors cette famille est aussi finie. Il est nécessaire que notre ensemble de fonctions soit fini car dans l’algorithme GI l’ensemble F doit être fini si nous voulons qu’il ait les bonnes propriétés.

Chaque sCSP pouvant être le résultat de l’application de fonctions du sCSP initial, on a besoin de toutes les fonctions de réduction (définis pour le problème initial sCSP) afin de modéliser les différentes exécutions possibles du processus de résolution.

En d’autres termes, considérons un sCSP y_i d’un sCSP Y; un ensemble de fonctions F’ peut s’appliquer sur y_i (à travers le processus de sélection de sCSP).

Si un nouveau sCSP y_j est créé (e.g., par découpage), alors les fonctions de F’ sont aussi requises pour être appliquées sur y_j.

Cependant, y_j pourra ne pas être créé. Notons qu’en théorie, il est nécessaire de prendre en compte tous les sCSP possibles (et ainsi, tous les ensembles possibles de sCSP possibles); malgré tout, en pratique, seules les fonctions utiles sont insérées dans l’algorithme GI.

Dans un premier temps, nous allons présenter les fonctions s’appliquant sur SCSP en accord avec les fonctions de sélection pour choisir les domaines sur lesquels seront appliquées les fonctions. Dans l’optique d’étendre les opérations de SCSP vers SCSP.

Considérons alors une fonction de sélection de domaine

Sel_D :SCSP → P(D)

et une fonction de sélection de sCSP :

Sel_y :SSCSP → SSCSP

Grâce à ces deux niveaux de sélection, nous pouvons détailler les choix réalisés par rapport au type de fonction que l’on souhaite appliquer.

6.6.2 Réduction de domaine

En se basant sur la notion de fonction de sélection de sCSP, nous pouvons définir un opérateur de réduction de domaines sur un sCSP comme :

red^Sel_D : SCSP → SCSP

y = (D,C,p) → (D’,C,p’)

tel que

D = D₁×...×D_n, D’ = D’₁×...×D’_n et ∀i, 1 ≤ i ≤ n
- D_i \not ∈ Sel_D(y) ⇒ D’_i = D_i
- D_i ∈ Sel_D(y) ⇒ D’_i ⊆ D_i
p’ = p si p ∈ LS_D’ sinon p’ correspond à n’importe quel échantillon pris dans ε(D’)

Notons que la condition 2. garantit que le chemin de recherche locale associé au sCSP reste dans ε(D’). Notons de même, que nous pouvons conserver p’=(s_i) où s_i est le plus petit élément de p appartenant à D’ ou nous pouvons conserver un sous-chemin approprié de p.

La fonction red^Sel_D est étendue à SCSP pour correspondre au choix du SCSP pris dans un ensemble SCSP :

red^{Sel_y, Sel_D} :

SCSP → SCSP

Y→ (Y\Sel_y (Y))

∪
y ∈ Sel_y(Y)

red^Sel_D(y)

Exemple : Réduction
Considérons un sCSP P = (D,C,p) avec D=(D_x,D_y), D_x = D_y = [1..10], C = { x < y} et p=(s₁) avec s₁ = (1,1). L’application d’une fonction de réduction de domaine sur ce sCSP provoque la suppression de la valeur 1 dans D_y. Dans ce cas l’échantillon associé au sCSP n’est plus valide dans le sCSP réduit et donc, par exemple, p’=(s₁’) avec s₁’ = (1,4) par tirage aléatoire d’une valeur dans D_y.

Ainsi par cette sélection double, nous pouvons matérialiser la réduction d’un domaine particulier sur un sCSP particulier. Voyons maintenant comment se définit un opérateur de découpage avec une sélection.

6.6.3 Découpage

Nous commençons par définir l’opérateur de découpage au premier niveau, sur un simple sCSP de la manière suivante :

sp^Sel_D_k : SCSP → SCSP
y→ Y’
avec y = (D₁×...×D_h×... ×D_n,C,p) où {D_h} = Sel_D(y) et
Y’ = {(D₁×...×D_h₁×...×D_n,C,p₁),...,(D₁×...×D_{h_k}×...×D_n,C,p_k)} tel que

D_h = U_i=1^k D_{h_i}
pour tout i ∈ [1..k], p_i = p si p ∈ LS_{(D₁×...× D_{h_i}×...×D_n)} sinon, p_i correspond à n’importe quel échantillon pris dans ε(D₁×...×D_{h_i}×...×D_n).

Nous présentons une fonction qui découpe un seul domaine d’un sCSP. Mais cette fonction peut être étendue pour un découpage de plusieurs domaines. La dernière condition est nécessaire pour respecter la définition de sCSP : elle correspond au fait que les échantillons associés au sCSP appartiennent à la boîte que forment leurs domaines. La fonction est étendue à SCSP, c’est-à-dire en passant par la sélection du sCSP, de la façon suivante :

sp^{Sel_y, Sel_D}_k :

SCSP → SCSP

Y→ (Y\Sel_y (Y))

∪
y ∈ Sel_y (Y)

sp^Sel_D_k(y)

6.6.4 La recherche locale

Comme nous l’avons vu, la recherche locale est assimilée à l’application de fonction sur un ordre partiel \sqsubseteq_ls; cet ordre est ensuite utilisé pour la définition de l’ordre \sqsubseteq de notre structure hybride SCSP. Les composants restant à définir sont les suivants :

la stratégie du calcul d’un chemin de recherche locale p’ de longueur n+1 depuis un chemin p de longueur n, et
le critère d’arrêt qui est communément basé sur un nombre limité de mouvements ainsi que, dans le contexte de la résolution de CSP, sur la notion de solution.

Pour débuter, nous définissons l’opérateur de recherche locale sur SCSP en tant que fonction strat :SCSP → P(ε(D)). Cette fonction caractérise la stratégie de choix de passage d’un échantillon à un de ses voisins pour une heuristique de recherche locale donnée .

l^strat_N :

SCSP → SCSP

y→ y’

où

N est le nombre maximum de mouvements autorisé
y = (C,D,p) et y’=(C,D,p’) avec p=(s₁,...,s_n)
1. p’=p si p ∈ Sol_{LS_D}
2. p’=p si n=N
3. p’=(s₁,...,s_n,s_n+1) tel que s_n+1 = strat(y) sinon

Notons que, encore une fois, ces fonctions satisfont les propriétés (inflationnaires et monotones) requises par l’algorithme GI. Puis, ces fonctions sont étendues à SCSP par:

l^Sel_y,strat_N :

SCSP → SCSP

Y→ (Y\Sel_y (Y))

∪
y ∈ Sel_y (Y)

l^strat_N(y)

6.6.5 Exemple de mouvement de recherche locale

Pour mettre en uvre ce schéma, nous présentons des exemples d’heuristiques de mouvement bien connues. Nous avons fait le choix de modéliser la relance (le restart pour une recherche locale afin d’effectuer une recherche depuis un nouvel élément initial) depuis un échantillon choisi aléatoirement après chaque réduction ou découpage. Considérons un sCSP y = (D,C,(s₁,...,s_n)). Chaque fonction consiste à sélectionner un voisin correct d’un échantillon (i.e., un échantillon du voisinage qui est aussi dans l’espace réduit D) :

Random Walk: la fonction strat_rw choisit aléatoirement un échantillon du voisinage du courant

strat_rw(y) = s t.q. s ∈ D ∩ N(s_n)
Descente: la fonction strat_d sélectionne un voisin qui améliore l’échantillon courant vis-à-vis de la fonction d’évaluation

strat_d(y) = s t.q. s ∈ D ∩N(s_n) et s < _eval s_n
Descente stricte: strat_sd est similaire à strat_d mais ne choisit que le meilleur voisin; strat_sd(y) = s t.q.

s ∈ D ∩N(s_n), s < _eval s_n, et ∀s’ ∈ D ∩N(s_n), s ≤ _eval s’
Tabou de taille l: sélectionne le meilleur voisin non visité durant les l derniers mouvements ; strat_{tabu_l}(y) = s t.q.

s ∈ ε(D) ∩N(s_n) et ∀j ∈ [n-l..n], s ≠ s_j et ∀s’ ∈ D ∩N(s_n), s ≤ _eval s’

6.6.6 Combinaison

La fonction de choix de l’algorithme GI, gère maintenant complètement la stratégie d’hybridation/combinaison. En effet, l’ensemble F est instancié par toutes les fonctions possibles applicables. Nous savons que, par les propriétés des fonctions (voir chapitre 5), différents ordonnancements de fonctions aboutissent au même résultat (en terme de point fixe).

En pratique, nous ne nous intéressons pas nécessairement à l’obtention du point fixe de l’algorithme GI. Nous pouvons en fait vouloir obtenir qu’un sCSP contienne une solution par la recherche locale ou par la propagation de contraintes. Auquel cas, si le but n’est pas l’obtention du point fixe global, différentes exécutions de l’algorithme GI avec différentes stratégies (fonctions de choix) peuvent mener à des solutions différentes (e.g., dans le cas des problèmes à solutions multiples ou de plusieurs optimums locaux).

Figure 6.3: Interaction entre voisinage et espace réduit

6.6.7 Résultat de l’algorithme GI

Présentons maintenant le résultat de l’algorithme GI pour les solutions d’un sCSP.

Du fait que nous sommes dans le cadre des itérations chaotiques (en ce qui concerne les ordre et les fonctions), étant donné un sCSP Y et un ensemble F de fonctions de réduction , l’algorithme GI calcule le plus petit point fixe commun des fonctions de F. Notons que ce résultat est garanti dans la mesure où nos fonctions LS limitent la taille des chemins et induisent un ordre partiel fini. Clairement, ce point fixe glfp(Y) caractérise toutes les solutions de Sol(Y):

U_{(d,C,p) ∈ Sol(Y)} d ⊇ U_{(d,C,p) ∈ glfp(Y)} d
pour tout (d,C,p) ∈ Sol(Y) t.q. p=(s₁, ..., s_n) ∈ Sol_{LS_D}(Y) il existe un (d,C,p’) ∈ glfp(Y) t.q. s_n ∈ ε(d).

Le premier point atteste que toutes les fonctions de réduction de domaines et de découpage utilisées dans GI conservent les solutions. Le second garantit que toutes les solutions calculées par les fonctions LS sont dans le point fixe de l’algorithme GI.

En pratique, on peut stopper l’algorithme GI avant l’obtention du point fixe. Par exemple, calculer le point fixe des fonctions de recherche locale ; dans ce cas, l’espace de recherche peut être réduit (et par là, les mouvements possibles) par l’application de certaines fonctions de réduction par propagation. Ceci correspond à la nature hybride de la résolution et aux compromis entre une exploration complète et incomplète de l’espace de recherche.

Exemple : Point fixe Dans l’exemple 8 la réduction d’un domaine a provoqué une réinitialisation de l’échantillon s₁ = (1,1) or le nouveau s₁’ = (1,4) fournit une solution possible au problème avant une réduction des domaines en singletons.

La figure 6.3 résume assez bien les interactions entre la réduction de l’espace par la propagation des contraintes et la structure de voisinage de la recherche locale. Dans un premier, nous allons illustrer ce cadre pour le problème du Sudoku en utilisant la Recherche Locale seule.

6.7 Application du modèle de recherche locale pour le Sudoku

Le jeu Sudoku a récemment atteint une popularité internationale, le succès de ce jeu vient probablement de la simplicité de ses règles : placer les chiffres de 1 à 9 dans une grille de 9 par 9 de telle sorte que chaque chiffre n’apparaît qu’une seule fois par ligne, par colonne et par région de 3 par 3(voir figure 6.4). Ce problème peut évidemment être considéré comme un problème de satisfaction de contraintes et ainsi nous servir de support pour tester notre modèle avec différentes méthodes de recherche locale.

Figure 6.4: Exemple de grille de Sudoku

Le Sudoku, généralisé à des grille de n² x n² à remplir avec les nombres de 1 à n², est NP-complet (preuve de [ Yato and Seta2002] par une simple réduction aux Carrés Latins). La populaire grille 9 ×9, divisée en régions de 3×3 est facile à résoudre avec un simple programme informatique. Par conséquent, afin d’augmenter la difficulté, nous considérons ici des grilles de 16×16 (publiées sous le nom de ßuper Sudoku"), 25×25 et 36×36.

Ce problème nous servira de support pour illustrer notre cadre générique. Nous verrons que nous pouvons facilement définir des algorithmes de recherche locale, les combiner et les comparer.

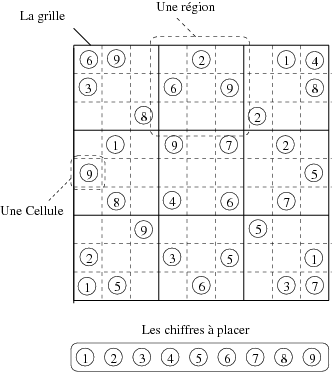
6.7.1 Le modèle CSP

Considérons un problème de taille n² x n², une formulation intuitive considère un ensemble de n⁴ variables qui correspondent aux cases à remplir. L’ensemble de contraintes est alors défini par des contraintes globales de type AllDiff (voir section 2.4.1, toutes les variables doivent avoir des valeurs différentes) représentant : chaque nombre apparaît une seule fois par ligne, une seule fois par colonne et une seule fois par région. Cette formalisation est telle que une grille de 36×36 équivaut à 1296 variables et 108 contraintes.

Les approches habituelles considèrent des grilles préremplies et les complètent, ou ont pour but de générer des grilles n’ayant qu’une seule et unique solution. Notre objectif ici est de générer des grilles complètes. Même si la programmation par contrainte est utilisée pour les petits problèmes, ce type d’approches complètes n’est pas applicable pour des instances plus grandes.

Nous considérons ici uniquement les grilles telles que tous les nombres apparaissent une seule fois dans chaque région n ×n. Ceci a pour but de mettre en uvre certaines contraintes directement dans le codage du problème et implique ainsi une restriction du voisinage à l’ensemble des échanges de cellules dans une même région. La fonction eval est liée à la notion de solution et est définie avec pour chaque contrainte AllDiff un degré de violation (le nombre d’affectation à corriger pour satisfaire la contrainte). Elle est donc égale à 0 si la contrainte est satisfaite. L’évaluation eval d’une grille est alors égale à la somme des degrés de violation de toutes les contraintes, elle est nulle si la grille satisfait toutes les contraintes.

6.7.2 Les fonctions

Nous retrouvons les notations précédentes, à savoir : un chemin de recherche locale p = (s₁,s₂,..,s_n) avec s_i une affectation, i.e. une grille remplie entièrement, ainsi que l’ordre sur ces chemins. Chaque affectation (instanciation de toutes les cellules de la grille) appartient à l’espace de recherche S, l’ensemble des grilles possibles. Nous n’allons pas effectuer ici de réduction de domaines, c’est pourquoi, pour une étude plus fine, nous détaillerons les aspects de la recherche. On note V le voisinage du dernier élément de p tel que V ⊆ N(s_n). L’ensemble V représente un sous ensemble des voisins possibles, car nous verrons par la suite que le voisinage diffère d’une méthode à une autre. De plus, nous avons besoin de définir une configuration de LS qui nous sera utile à la définition des différentes méthodes de recherche locale. Nous appelons configuration de recherche locale le couple (p,V) avec p = (s₁,s₂,..,s_n) et V ⊆ N(s_n). Ce couple ne change en rien l’ordre qui sera défini uniquement sur p comme précédemment. Ainsi, les fonctions de voisinage que nous allons décrire correspondent à des fonctions d’une configuration à une autre (p,V) → (p,V UV’), le voisinage sera différent selon la méthode utilisée.

En ce qui concerne les méthodes, la recherche tabou (TS) [ Glover and Laguna1997] a été appliquée avec succès pour la résolution de CSP. Cet algorithme interdit les mouvements vers des affectations déjà visitées lors des l derniers pas de recherche. Nous considérons de même la descente avec marche aléatoire (RW) où les mouvements s’effectuent avec une certaine probabilité (notée \mathfrakpb).

Selon notre modèle, nous devons uniquement décrire les fonctions qui seront utilisées dans l’algorithme générique pour modéliser les différentes stratégies. Les fonctions de voisinage sont des fonctions de (p,V) → (p,V UV’) répondant aux conditions suivantes :

VoisinageComplet :

p = (s₁,...,s_n) et V’ = {s ∈ N(s_n) | s \not ∈ V }

VoisinageTabou :

p = (s₁,...,s_n) et V’ = {s ∈ N(s_n)| \not ∃k, n-l ≤ k ≤ n, s_k=s }

VoisinageDescente :

p = (s₁,...,s_n) et V’ = {s ∈ N(s_n) t.q. \not ∃s’ ∈ V, eval(s’) < eval(s)

Les fonctions de mouvement sont des fonctions cette fois de (p,V)→ (p’,Æ) avec p = (s₁,s₂,..,s_n) et p’ = (s₁,s₂,..,s_n,s_n+1) représentant le fait qu’un point s_n+1 est ajouté au chemin de recherche avec son voisinage initialement vide :

MouvementMeilleur :	s_n+1 = s’ t.q. eval(s’) = min_{s" ∈ V} eval(s")
MouvementAméliore :	s_n+1 = s’ t.q. eval(s’) < eval(s_n) et s’ ∈ V
MouvementAléatoire :	s_n+1 = s’ t.q. s’ ∈ V

Nous pouvons alors préciser l’ensemble de fonctions F comme entrée de l’algorithme GI.

Recherche Tabou :	{ VoisinageTabou ; MouvementMeilleur }
Marche Aléatoire :	{VoisinageComplet ; MouvementMeilleur
	;MouvementAléatoire }
Recherche Tabou + Descente :	{ VoisinageTabou ; VoisinageDescente
	; MouvementAméliore ; MouvementMeilleur }
Marche Aléatoire + Descente :	{ VoisinageComplet ; MouvementMeilleur
	; MouvementAléatoire ; VoisinageDescente
	; MouvementAméliore }

Pour l’algorithme de marche aléatoire, étant donné un paramètre probabilité \mathfrakpb, nous introduisons un quota de \mathfrakpb fonctions MouvementMeilleur et donc 1-\mathfrakpb de fonctions MouvementAléatoire dans le GI. Concernant la recherche tabou, nous utilisons une liste l de taille 10 et les fonctions VoisinageTabou et MouvementMeilleur. Enfin, nous combinons les stratégies précédentes avec de la descente en ajoutant les fonctions VoisinageDescente et MouvementAméliore. Remarquons que les différents algorithmes correspondent ici aux différents ensembles de fonctions et aux différents comportements de la fonction choisir de l’algorithme GI. La fonction choisir sélectionne alternativement fonction de voisinage et fonction de mouvement.

6.7.3 Résultats expérimentaux

Dans le tableau 6.1, nous comparons les résultats obtenus avec la recherche tabou et la marche aléatoire associées à la descente sur différentes instances (tailles) du Sudoku. Nous avons préalablement mesuré la difficulté du problème par une méthode complète classique avec propagation et découpage. Nous avons alors obtenu un temps de calcul supérieur à un jour pour une grille 36×36.

Á l’opposé, par une simple formulation du problème et grâce au modèle d’application des fonctions, nous sommes capables d’atteindre une solution avec une recherche locale classique, et ce depuis une grille vide. Pour chaque méthode et chaque instance, nous avons effectué 2000 exécutions, excepté pour le problème 36×36, 500 exécutions.

Les résultats obtenus par ajout de la descente dans la recherche tabou ou la marche aléatoire, montrent une réduction du temps de calcul pour atteindre une solution. Nous remarquons alors, qu’une stratégie hybride combinant plusieurs fonctions de mouvement et de voisinage fournit de meilleurs résultats. Notre cadre nous permet d’accorder au mieux un équilibre entre différentes fonctions de bases qui caractérisent des stratégies de résolution basiques. Ainsi, nous pouvons élaborer une grande variété d’algorithmes dans un simple algorithme générique.

	Recherche Tabou			Marche Aléatoire
n² x n²	16x16	25x25	36x36	16x16	25x25	36x36
temps cpu moy.	3,14	115,08	3289,8	3,92	105,22	2495
écart type	1,28	52,3	1347,4	1,47	49,3	1099
Nbr de mvts	405	3240	22333	443	2318	13975
	Descente + Recherche Tabou			Descente + Marche Aléatoire
n² x n²	16x16	25x25	36x36	16x16	25x25	36x36
temps cpu moy.	2,34	111,81	2948	2,41	82,94	2455
écart type	1,42	55,04	1476	1,11	36,99	1092
Nbr de mvts	534	3666	20878	544	2581	14908

Table 6.1: Résultats du Sudoku par différentes méthodes de recherche

6.8 Application du modèle pour une hybridation CP+LS

Pour tester notre modèle d’hybridation nous avons sélectionné des problèmes classiques différents : S+M=M (Send + More = Money), leCarré magique, Langford numbers, le problème du Zèbre, la règle de Golomb, et l’Uzbekian problem, issus de la CSPlib [ Gent et al. ].

6.8.1 Fonctions et stratégies

Nos fonctions de bases sont réparties en trois ensembles : un ensemble des fonctions de réduction dr, un ensemble des fonctions de découpage sp, et un ensemble pour les fonctions de recherche locale ls.

La fonction de choix dans l’algorithme GI est définie ainsi : soit un tuple (a, β, g) tel que a, b, et g représentent respectivement le pourcentage de fonctions de réduction, de fonctions de découpage, et de fonctions de recherche locale, qui est appliqué ; les fonctions sont sélectionnées équitablement avec ces ratios.

Les fonctions de réduction sont définies de la façon suivante :

une fonction de réduction de domaine correspond soit à une réduction à une consistance de bornes ou soit à un opérateur de filtrage pour une contrainte globale ( (e.g., AllDiff),
une fonction de découpage coupe un domaine sélectionné en deux sous-domaines.
une fonction de recherche locale est un mouvement de base : les fonctions LS sont ensuite instanciées pour une stratégie de recherche tabou, laquelle sélectionne le meilleur voisin qui n’est pas dans la liste de taille 10.

Par la suite, nous considérons trois types de stratégies correspondant aux fonctions de sélection de sCSP (pour sélectionner un sCSP dans un sCSP, i.e., la fonction Sel_y comme définie en section 6.6), et

une fonction de sélection de domaine (pour sélectionner un domaine dans un CSP, i.e., la fonction Sel_D) pour la réduction de domaine et le découpage. Nous n’allons pas ici formuler ces fonctions, mais uniquement en décrire les stratégies :

random: Sel_y choisir aléatoirement un sCSP, et Sel_D choisir n’importe quel domaine du sCSP sélectionné.
depth-first: Sel_y choisir le sCSP qui contient le plus petit domaine, et Sel_D choisit le plus petit domaine du sCSP.
LS-forward checking: le forward checking consiste à instancier les variables dans un ordre donné et d’anticiper sur les conflits futurs en réduisant les variables liées directement à celle venant d’être énumérée. Notre stratégie LS-forward checking est similaire; les fonctions ls seront appliquées sur le sCSP qui vient d’être découpé.
width-first: Sel_y choisir le sCSP qui contient le plus grand domaine, et Sel_D choisit le plus grand domaine du sCSP sélectionné.

Par une combinaison de nos fonctions de réduction et des trois stratégies décrites ci-dessus, nous obtenons un triplet (pour chaque stratégie) d’ensembles de fonctions (dr, sp, et ls).

6.8.2 Résultats expérimentaux

L’évaluation et les critères de comparaison correspondent au nombre de fonctions de bases appliquées pour atteindre une première solution. Une telle application de fonction est soit : un pas de recherche locale, soit un découpage, ou soit une réduction de domaine (réduction d’un domaine en utilisant une contrainte).

Nous étudierons des petits problèmes (voir les définitions des problèmes au chapitre 1.4), pour lesquels le temps de calcul ne dépasse pas une minute (e.g., une solution pour le nombre de Langford est trouvée en une seconde).

Interactions entre CP et LS

Nous utilisons différentes stratégies afin d’étudier les bénéfices de l’hybridation CP+LS, les effets des différentes coopérations sur l’efficacité de la résolution.

Commençons par les problèmes du nombre de Langford et S+M=M; les tests sont réalisés en augmentant le pourcentage a de propagation de 0 à 100%. Pour garantir l’obtention de solution, nous imposons un ratio de découpage β = a* 0.1. Par exemple, si a = 40%, nous avons alors β = 4% de découpage , et ainsi 56% de LS. Ces tests utilisent la stratégie en profondeur d’abord (depth-first).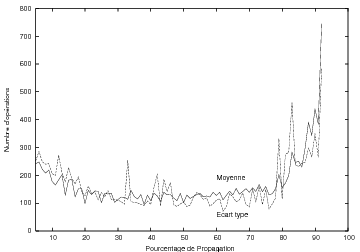

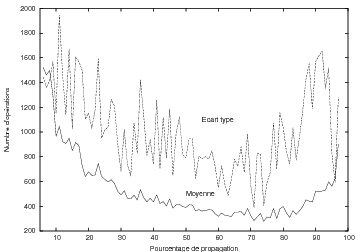
Figure 6.5: Coût d’une solution : nombre de Langford (Depth-First)

La figure 6.5 montre que les meilleurs résultats pour le nombre de Langford correspondent à une gamme du ratio de propagation entre 35% et 45%. En fait, quand la recherche locale représente moins de 10% de l’effort de recherche, atteindre une solution, équivaut à calculer le point fixe pour la propagation de contrainte (i.e., appliquer toutes les fonctions de propagation). Notons que, pour ce problème, la recherche tabou seule (figure 6.5, à gauche) fournit de meilleurs résultats que la propagation avec le découpage (figure 6.5, à droite).

Figure 6.6: Coût d’une solution : Send+More=Money (Depth-First)

La figure 6.6 représente les résultats obtenus par la stratégie depth-first pour résoudre le problème S+M=M. L’écart type est important : en effet, bien que les sCSP et les domaines soient sélectionnés, le choix de la fonction à appliquer n’est pas fixe. Néanmoins, en moyenne, les exécutions sont plus stables et la meilleure gamme correspond à 70%- 80% de propagation. Ici, LS seule (figure 6.6, à droite) apparaît moins efficace que CP (figure 6.6, à gauche).

	S+M=M	LN42	Zèbre	Carré Magique	Golomb
	70-80	15 - 25	60-70	30-45	30 - 40

Table 6.2: Meilleures gammes du taux de propagation pour calculer une solution

Ainsi, choisir les meilleurs ratios pour une hybridation, dépend du problème et de la stratégie appliquée. Le tableau 6.2 présente les meilleures gammes avec la stratégie LS-Forward-checking sur les différents problèmes. Les résultats illustrent le fait que l’introduction progressive de CP dans LS (idem pour LS dans CP) mène à une résolution plus efficace. Les ratios de l’hybridation peuvent ainsi être définis pour optimiser les performances.

Bénéfice de l’hybridation par rapport à LS seule et CP seule

Le tableau 6.3 présente une étude comparative entre l’hybridation CP+LS, CP seule, et LS seule :

les trois stratégies mentionnées précédemment (random, depth-first, LS forward checking)
CP+LS: les ratios (a,b,g) sont les meilleurs ratios sélectionnés dans le tableau 6.2,
CP (seule): les rations sont (90%,10%,0),
LS (seule): les ratios sont (0,0,100%).

Stratégie	Méthode	S+M=M	LN42	Carré magique	Golomb
Random	LS	1638	383	3328	3442
	CP+LS	1408	113	892	909
	CP	3006	1680	1031	2170
D-First	LS	1535	401	3145	3265
	CP+LS	396	95	814	815
	CP	1515	746	936	1920
FC	LS	1635	393	3240	3585
	CP+LS	22	192	570	622
	CP	530	425	736	1126

Table 6.3: Nombre moyen d’opérations pour calculer une première solution

6.9 Conclusion

Les résultats montrent les bénéfices de l’hybridation grâce aux interactions entre les méthodes de résolution. Les améliorations apparaissent sur des problèmes pour lesquels LS est meilleure que CP, mais aussi pour des problèmes où CP est meilleure que LS. De plus, l’efficacité est étroitement liée à la structure du problème (telle que la densité de solutions) et à la stratégie choisie. Les expérimentations avec la stratégie en largeur d’abord (Width-First strategy) mentionnée plus tôt ne sont pas présentées ici, mais fournissent des résultats similaires.

Dans ce chapitre, nous avons présenté un modèle pour intégrer différentes stratégies de combinaison et en prouver quelques propriétés. Nous avons montré que notre travail peut servir de base à l’intégration de méthodes LS et CP afin de mettre en valeur les connexions entre techniques complètes et incomplètes. Dans ce contexte, les propriétés liées aux solveurs (telles que par exemple la terminaison, les solutions) peuvent facilement être exprimées et établies. Ce cadre de travail permet en outre d’envisager de nouvelles stratégies de combinaison et d’étudier les combinaisons d’algorithmes de recherches locale entre eux.

Chapitre 7

Modèle hybride pour

les algorithmes génétiques

Dans ce chapitre, nous présentons une hybridation de méthodes complètes, mais cette fois avec les algorithmes génétiques. La démarche proposée au chapitre 6 est alors appliquée à cette classe des métaheuristiques pour être utilisée dans un contexte d’optimisation sous contraintes.

7.1 Introduction

Nous voulons utiliser un cadre uniforme nous permettant de combiner des techniques de propagation de contraintes et les algorithmes génétiques. Basés sur le principe de la sélection naturelle, les algorithmes génétiques ont été appliqués avec succès aux problèmes combinatoires tels que les problèmes d’ordonnancements ou de transports. L’application d’un algorithme génétique consiste en la génération successive de meilleurs individus en fonction du problème choisi. Nous devons définir les composants suivants (voir chapitre 3) :

une représentation des solutions potentielles (les individus),
une manière de créer une première population,
une fonction d’évaluation eval.
les opérateurs génétiques qui définissent la composition des enfants: deux opérateurs différents seront ici considérés: le croisement et la mutation.
un ordre sur les populations pour une intégration dans le cadre.

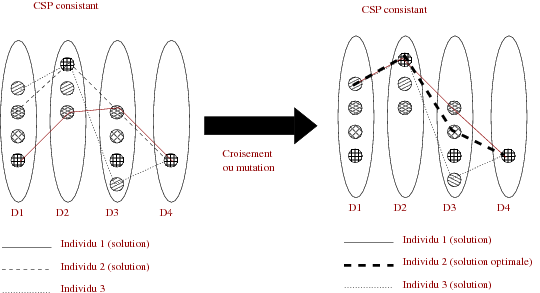
Une fois clairement présentés, les algorithmes génétiques seront alors couplés aux méthodes complètes, puis appliqués à un problème d’optimisation sous contraintes. L’idée (voir figure 7.1) est que la partie optimisation sera alors intégrée à la fonction d’évaluation eval mentionnée plus tôt. Cette fonction sera ensuite utilisée par l’algorithme génétique pour trouver une solution optimale.

Figure 7.1: Algorithme génétique pour l’optimisation

7.2 Algorithme génétique et population

7.2.1 Populations

Les algorithmes génétiques ont pour but de générer de nouvelles populations via des opérateurs génétiques, sélection [ Bäck et al. 2001], (e.g. sélection proportionnelle [ Holland1975a], sélection avec roulette [ Goldberg1989a], sélection par tournois, linear ranking [ Baker1985], ...), recombinaison (e.g., recombinaison élitiste [ Thierens and Goldberg1994], recombinaison multiparents [ Eiben et al. 1994]), et mutation.

Une nouvelle population sera appelée une descendance et peut être vue comme une application :

O : P(D) → P(D)

Nous définissons l’ensemble des descendances possibles, i.e., l’ensemble des suites de populations comme suit :

GA =

∪
k > 0

{ p = (g₁,...,g_k) | ∀j ∈ [1..k], g_j ∈ P(D) et ∀j ∈ [2..k], g_j ∈ O(g_j-1)}

Où g₁ représente la population initiale et k la longueur du processus. Notez qu’en pratique la taille de chaque population est fixée.

7.2.2 Ordre sur les individus, ordre sur les populations

En pratique, comme pour la recherche locale, les algorithmes génétiques sont limités par un critère d’arrêt, lequel correspond pour une majorité des cas, à un nombre maximum d’itérations, i.e., un nombre maximum de générations. Donc, en ce qui concerne les AG, un résultat est soit une population g contenant des solutions ou soit le processus de recherche a atteint le nombre maximum d’itération. Concernant l’évaluation des solutions potentielles, la fonction eval sera utilisée sur les échantillons pour mesurer la qualité des affectations (nombre de contraintes violées). Mais aussi, puisque nous sommes dans le contexte de l’optimisation sous contraintes, cette fonction prend également en compte l’évaluation par la fonction objectif.

La fonction eval peut être définie de la manière suivante :

eval :

D → (ℵ,\RR)

s → (e,r)

Où pour un élément (individu) s de l’espace de recherche, (e) est le nombre de contraintes violées et (r) son évaluation par la fonction objectif correspondant au problème.

Cette définition peut être étendue aux populations par :

eval :

P(D) → \RR

g → r

Où r correspondrait à un évaluation globale (agrégation) de la qualité des individus de g.

Basé sur une fonction d’évaluation, nous introduisons l’ordre suivant sur la séquence de populations de GA :

Définition 29 [Relation sur les séquences de populations]
Considérons une fonction d’évaluation eval. La relation d’ordre \sqsubseteq_ga sur GA est défini de la façon suivante :

(g₁, ..., g_n) \sqsubseteq_ga (g₁’, ..., g’_m) ssi g’_m ≤ _eval g_n

Le coupe ( GA,\sqsubseteq_ga) forme un pré-ordre puisque deux populations différentes ayant la même valeur par l’évaluation se voient comparables dans les deux sens.
Il nous faut maintenant définir la structure de calcul sur laquelle les fonctions de réduction vont s’appliquer, incluant les nouveaux composants de recherche locale et des algorithmes génétiques.

7.2.3 Structure de calculs

Afin de rendre compte des différentes structures de données associées à chaque technique de la résolution hybride, nous complétons le modèle CSP en lui ajoutant un facteur génétique. Ce facteur correspond au processus génétique et c’est par lui que se fera l’optimisation.

Commençons par définir la structure de calcul vouée à l’hybridation CP+AG.

Définition 30 [CSP avec facteur génétique] Un CSP avec un facteur génétique pour l’optimisation (gCSP) est défini par une séquence (D,C,p,f) où :

D = D₁×...×D_n

∀c ∈ C, c ⊆ D₁ ×... ×D_n

p ∈ GA

f: fonction objectif.

GCSP désigne l’ensemble de gcsp, et SGCSP l’ensemble P(GCSP)
Remarquons, que dans cette définition, le processus d’algorithme génétique p doit être inclus dans l’espace de recherche défini par D. Rappelons que la fonction objectif f est prise en considération via la fonction eval, et est ainsi prise en compte pour les ordre ≤ _eval et \sqsubseteq_ga, et par conséquent dans la structure ordonnée (GCSP,\sqsubseteq) définie plus tôt.

Définition 31 [Relation sur GCSP]

Étant donnés deux gcsp y = (D,C,p,f) et y’=(D’,C,p’,f), y\sqsubseteq y’ ssi

D’ ⊆ D

ou (D’ = D et p \sqsubseteq_ga p’).

Cette relation est étendue sur P(GCSP): {f₁;...;f_k} \sqsubseteq {y₁;...;y_l}, ssi

∀f_i, (∃y_j, f_i\sqsubseteq y_j et \not ∃y_j, y_j\sqsubset f_i)

où i ∈ [1..k],j ∈ [1..l].
SGCSP (i.e., l’ensemble P(GCSP)) constitue l’ensemble clé de la structure de calculs. Nous utilisons sCSP pour désigner un élément de SGCSP. Le plus petit élément ⊥ est {(D,C,p,f)}, i.e., le sCSP initial à résoudre.

7.2.4 Les solutions

En ce qui concerne la programmation par contrainte, une solution d’un gcsp y = (D,C,p,f) est un tuple qui satisfait toutes les contraintes. Mais pour les algorithmes génétiques, la notion de solution est liée à la fonction d’évaluation : une solution est décrite comme un élément s d’une population g de la séquence p de sorte qu’à s est assignée la plus petite valeur (ou la plus grande) de la fonction objectif par rapport à tous les autres s’ contenus dans p.

Étant donné un gcsp y = (D,C,p,f), ces deux points de vue induisent deux ensembles de solutions :

Solutions réalisables : Sol_CP(y) = { d ∈ D | ∀c ∈ C, d ∈ c }
Solutions optimales : Sol_GA(y) = {s | p = (g₁,...,g_m) et ∀i ∈ [1..m], ∀s’ ∈ g_i, s ≤ _eval s’ pour une minimisation (resp. s’ ≤ _eval s pour une maximisation )}

En se basant sur ces définitions, nous définissons l’ensemble des solutions dans le modèle hybride pour un gcsp donné par :

Sol(y) = Sol_CP(y) ∩Sol_GA(y)

Désormais, une solution d’un gcsp est un tuple d tel que d satisfait les contraintes et minimise (resp. maximise) la fonction objectif. Cette notion de solution est généralisée sur la structure de calculs SGCSP.

Définition 32 Soit un sCSP Y = {y₁,...,y_k} pour

un problème de minimisation : Sol(Y) = Min({s_i} | s_i ∈ sol(y_i) }

un problème de maximisation : Sol(Y) = Max({s_i} | s_i ∈ sol(y_i) }

Fournissons maintenant les propriétés de certaines des algorithmes génétiques.

Définition 33 [Élitisme]
Un algorithme génétique est dit élitiste si, à chaque étape, le meilleur individu survit, la meilleure solution n’est donc jamais perdue durant le processus de recherche. Formellement, considérons un chemin de recherche p = (g₁,...,g_k):

∀j ∈ [1..k-1], si il existe s ∈ g_j t.q. ∀s’ ∈ g_j, s ≤ _eval s’, alors s ∈ g_j+1

On obtient alors, pour un algorithme génétique élitiste, que si pour chaque population g il y a une probabilité non nulle P qu’à la génération suivante la population est meilleure :

∀s ∈ g_k, ∃s’ ∈ g_k+1 t.q. s’ ≤ _eval s

Le résultat de l’évaluation de la population au temps t converge vers la valeur optimale, pour t → ∞.

7.2.5 Un système à base de fonctions

Á ce stade, nous devons définir les fonctions de réduction sur SGCSP. Elles décrivent les différents composants du processus de résolution : la propagation de contraintes par réduction des domaines et le découpage, combiné aux algorithmes génétiques.

Soit un élément Y = {y₁,...,y_n} de SGCSP, nous appliquons des fonctions sur Y correspondant à la réduction de domaines, au découpage des domaines, et aux algorithmes génétiques. Ces fonctions sont susceptibles de s’appliquer sur différents éléments y_i de Y, ainsi que pour chaque y_i sur certain de ses composants. Notons que dans la mesure où nous considérons des ensembles finis pour le gcsp initial, la structure forme un ordre partiel fini.

Les définitions qui vont suivre introduisent les propriétés fondamentales des différents opérateurs ainsi que leurs objectifs.

Les définitions de réduction de domaines et de découpage pour une hybridation CP+AG sont similaires de celles pour CP+LS (Definitions 26 et 27). Cependant, cette fois elles s’appliquent sur SGCSP. La remarque est identique concernant les définitions 36 et 28.

Définition 34 [Fonction de réduction de domaines] Une fonction de réduction de domaines red est une fonction :

red :SGCSP → SGCSP

{y₁, ..., y_n} → {y’₁,..., y’_n}

telle que ∀i ∈ [1...n ]:

soit y_i = y’_i,

ou soit y_i = (D,C,p,f), y’_i = (D’,C,p’,f) et D ⊇ D’ et Sol(y_i) = Sol(y’_i).

Cette définition garantit que {y₁, ..., y_n}\sqsubseteq red({y₁, ..., y_n}) et que la fonction est inflationnaire et monotone sur (SGCSP,\sqsubseteq) .

Du point de vue de la programmation par contraintes, une solution ne peut être perdue par une fonction de réduction de domaines. Ce qui est le cas pour une fonction de découpage définie de la façon suivante.

Définition 35 [Découpage de domaines]
Une fonction de découpage de domaines sp sur SGCSP est une fonction telle que pour tout Y = {y₁, ..., y_n} ∈ SGCSP:

a. sp(Y)={y’₁, ..., y’_m} avec n ≤ m,
b. ∀i ∈ [1..n],

soit ∃j ∈ [1..m] tel que y_i = y’_j

ou soit il existe y’_j₁, ..., y’_{j_h}, j₁, ..., j_h ∈ [1..m] tels que

Sol_D(y_i) =
∪
k=1..h
Sol_D(y’_{j_k})

c. et, ∀j ∈ [1..m],

soit ∃i ∈ [1..n] tel que y_i = y’_j

ou y’_j = (D’,C,p’,f) et il existe y_i = (D,C,p,f), i ∈ [1..n] tel que D ⊇ D’.

Les conditions a. et b. garantissent que des gcsp ont été découpés sans écarter la moindre solution. La condition c. garantit que l’espace de recherche n’augmente pas (chaque nouvel espace de recherche est inclus dans l’espace de recherche initial).

De plus, lors d’une réduction par découpage ou une réduction de domaine, si des individus n’appartiennent plus à l’espace de recherche défini par le sCSP, la population est réparée en complétant les individus de manière aléatoire, ou l’algorithme dispose d’une heuristique particulière pour la création de nouveaux individus.

Nous définissons enfin les processus génétiques en tant que fonctions de réduction sur SGCSP.

Définition 36 [Algorithmes génétiques]

Une fonction algorithme génétique G_N est une fonction : G_N :SGCSP → SGCSP,
{y₁, ..., y_n} → {y’₁,..., y’_n} où N est le nombre maximum de générations successives, et ∀i ∈ [1..n]

soit y_i=y’_i

ou soit y_i=(D,C,p,f) et y_i’=(D,C,p’,f) avec p=(g₁,...,g_k)
et p’=(g₁,...,g_k,g_k+1) tel que g_k+1 ∈ O(g_k) ∩D^m et k+1 ≤ N, où m est la taille de la population.

N est la taille maximale de l’algorithme génétique, i.e. le nombre de génération autorisé dans le cadre d’une recherche génétique classique. Notons que y_i=y’_i peut être observé quand :

n=N: le nombre maximum d’opérations est atteint,
G_N est la fonction identité sur y_i, i.e., G_N n’essaye plus d’améliorer la génération du GCSP y_i. Ceci peut apparaître lorsque plus aucun mouvement ne peut être effectué (e.g., tous les individus sont égaux et la mutation n’est pas permise).

Grâce aux propriétés précédentes, l’algorithme optimise la fonction objectif, prenant ses valeurs dans un espace de recherche de plus en plus consistant avec CP. Par applications successives des fonctions de propagation de contraintes et de découpage, l’espace de recherche est progressivement restreint aux solutions réalisables et donc AG trouve l’optimum.

7.2.6 La résolution sGCSP

L’ordre sur SGCSP est fourni à l’algorithme GI, le plus petit élément ⊥ correspond à {(D,C,p,f)}, i.e., le sGCSP initial à résoudre, sont fournies aussi les fonctions monotones et inflationnaires : réduction de domaines, découpage et algorithmes génétiques.

Les fonctions de réduction sont dans un premier temps construites sur GCSP avant d’être étendues sur SGCSP. Dans ce cas, un processus de sélection est nécessaire pour prendre en compte chaque sGCSP pouvant être généré pendant la résolution. Nous n’allons pas détailler ici ce processus du fait qu’il s’agit du même que celui de l’hybridation avec la recherche locale.

Résultat de l’algorithme générique itératif

Le résultat de l’algorithme GI peut être décrit de manière analogue à celle fournie précédemment. Étant donnés un sGCSP Y et un ensemble F de fonctions de réduction, l’algorithme GI calcule le plus petit point fixe commun des fonctions de F. La figure 7.2 nous montre comment, à partir des contraintes, des opérateurs sous la forme de fonctions de réduction sont appliqués. Nous remarquons que dans cette représentation, la solution optimale peut éventuellement être obtenue par AG avant l’obtention du point fixe global des fonctions de F (qui en fournira alors la preuve), cependant ce point fixe, noté glfp(Y), procure toutes les solutions de Sol(Y) définies par :

U_{(d,C,p) ∈ Sol(Y)} d ⊇ U_{(d,C,p) ∈ glfp(Y)} d
pour tout (D,C,p,f) ∈ Sol(Y) t.q. p=(g₁, ..., g_n) ∈ Sol_{GA_D}(Y) il existe un (d,C,p’,f) ∈ glfp(Y) t.q. ∃i ∈ [1..n], d ∈ g_i.

Figure 7.2: Schéma général d’application des fonctions pour l’hybridation CP+GA

Le premier item consolide le fait que les fonctions de réduction et de découpage utilisées, protègent les solutions. Le second garantit que dans toutes les séquences de populations, qui sont solutions de l’algorithme génétique, il y a une population contenant un tuple qui est dans le point fixe de l’algorithme GI.

7.3 CP+AG pour les problèmes d’optimisation

7.3.1 Instances du problème

Le problème d’équilibrage des diplômes (BACP : Balanced Academic Curriculum Problem) est une classe de problèmes issue de la CSPlib [ Gent et al. ]. Il consiste à planifier les cours composant un diplôme afin d’équilibrer la charge des étudiants pour chaque période scolaire. Chaque cours est doté d’un certain nombre de crédits représentant la quantité de travail nécessaire pour le suivre avec succès. La charge d’une période est la somme des crédits de chaque cours de la période. D’autres contraintes sont ajoutées : une charge maximale et minimale par période, et des rapports de précédence sont établis entre certains cours (figure 7.3).

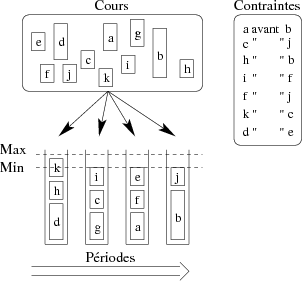
Figure 7.3: Exemple de distribution des cours.

Le problème d’équilibrage des programmes est décrit comme suit:

Un nombre de cours m, un nombre de périodes n : chacun des m cours doit être affecté à une des n périodes,
une charge académique c_i : pour chaque cours i, un nombre de crédits (coût),
des prérequis (contraintes de précédence) : certain cours peuvent nécessiter d’autre cours en prérequis (e.g. le cours b a le cours a comme prérequis : x_a < x_b),
β charge académique minimum : un nombre minimum de crédits par période est nécessaire,
g charge académique maximum : un nombre maximum de crédits par période est autorisé pour éviter la surcharge horaire,
δ nombre minimum de cours : un nombre minimum de cours par période est nécessaire,
ε nombre maximum de cours : un nombre maximum de crédits par période est autorisé pour éviter la surcharge de travail.

Une solution est alors une affectation équitable des cours aux différentes périodes, ce que nous traduisons comme une minimisation de la période la plus chargée.

Nous considérons ici, différentes instances du BACP : bacp8, bacp10, et bacp12, c’est-à-dire les problèmes pour 8, 10 et 12 périodes extraits de la CSPlib [ Gent et al. ]; et finalement, les données de ces trois diplômes seront utilisées pour former un nouveau problème (bacpall) dans lequel certains cours seront partagés par les différents diplômes.

Par exemple, pour le problème à 10 périodes, 42 cours doivent être distribués sur les 10 périodes. Chaque cours a un crédit qui selon le cours en question varie entre 1 et 5. Le nombre de contraintes de précédence est de 32, chaque période doit avoir entre 2 et 10 cours et une charge (somme des crédits) entre 10 et 24.

7.3.2 Processus expérimental

Comme pour CP+LS, nos fonctions de bases sont organisées en trois ensembles : l’ensemble des fonctions de réduction dr, l’ensemble des fonctions de découpage sp, et l’ensemble des fonctions d’algorithmes génétiques ga. Dans ce qui suit, la stratégie de profondeur d’abord est utilisée.

Les fonctions de réduction correspondent à des opérateurs d’arc consistance pour les contraintes binaires de précédence entre les cours et de réduction de contraintes globales (e.g., period,load) sont utilisées pour modéliser les problèmes et élaguer l’arbre de recherche en détectant les inconsistances. Les contraintes globales period(i,δ,ε) calculent le nombre de domaines avec la valeur i. Si moins de j occurrences de i sont présentes dans les m domaines alors le CSP courant est localement inconsistant :

δ ≤ (

m
∑
k=1

1 | x_k = i) ≤ ε

Les contraintes globales load(i,b,g) calculent elles, la charge pour une période donnée i du CSP courant :

β ≤ (

m
∑
k=1

c_k | x_k = j) ≤ g

sp sont les opérateurs de découpage, coupant un domaine sélectionné en deux sous-domaines.

Figure 7.4: fonctions ga

ga regroupe les opérateurs génétiques de base (voir figure 7.4) instanciés dans notre algorithme génétique. Depuis une population k, notre algorithme génère une population k+1 de 60 individus sélectionnés parmi 100 issus de k et ceci à chaque appel de ga. Lorsque ga est appelé par l’algorithme principal, les cas suivants peuvent se présenter :

la population k+1 a moins de 100 individus: un individu est sélectionné aléatoirement, puis est soit couplé avec un autre parent pour créer deux enfants dans k+1, soit est victime d’une mutation ou demeure inchangé.
la population k+1 a 100 individus: les 60 meilleurs sont sélectionnés selon la fonction d’évaluation qui prend en compte la fonction objectif.

7.3.3 Résultats expérimentaux

Pour les expérimentations, nous avons intégré le module AG (i.e., ga fonctions) dans notre système à base de contraintes pour l’hybridation. De même, nous avons ajouté la notion d’optimisation à la simple notion de solution.

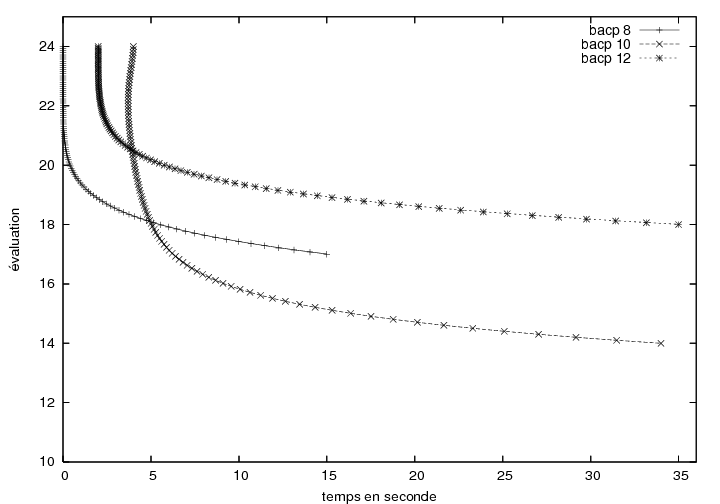
Figure 7.5: Évolution des fonctions de coût

Dans le but de comparer nos résultats, nous présentons les résultats obtenus par [ Castro and Manzano2001] utilisant un solveur en programmation linéaire lp_solve pour les instances bacp8 et bacp10 du problème (la table 7.1 montre l’évolution du coût de l’évaluation de la fonction objectif en fonction du temps de calcul). Les résultats de notre solveur hybride CP+AG sont présentés dans la table 7.2. Nous observons qu’en dépit du fait que lp_solve est capable de trouver la valeur optimale pour le premier problème, ce n’est pas le cas pour le second.

Qualité sol.	bacp 8	Qualité sol.	bacp 10
24	137.08	33	9.11
23	218.23	32	25.38
21	218.43	30	25.65
20	712.84	29	1433.18
19	1441.98	27	1433.48
18	1453.73	26	1626.49
17 (optimum)	1459.73	24	1626.84

Table 7.1: Résultats en seconde avec lp_solve

Qualité sol.	bacp 8	bacp 10	bacp 12
24	0.47	4.71	2.34
23	0.54	4.67	2.40
22	0.61	3.68	2.48
21	0.61	4.36	2.76
20	0.69	4.63	3.20
19	0.83	4.95	4.25
18	1.20	5.13	35.20
17	15.05 (optimum)	5.60
16		6.39
15		8.53
14		34.84 (optimum)

Table 7.2: Résultats avec GA+CP

La figure 7.5 nous montre l’évolution des différentes fonctions d’évaluation selon les problèmes, nous observons pour chacune d’elles une convergence plus moins rapide vers son optimum global.

Comme mentionné plus tôt, nous contrôlons les taux pour chaque famille de fonctions dr, sp et ga pour définir la stratégie , par un tuple (%_dr,%_sp,%_ga) de ratio d’applications.

Ainsi, ces valeurs correspondent aux probabilités d’application d’une fonction pour chaque famille. En pratique, nous mesurons en figures 7.6 le taux d’applications efficaces, i.e., nous comptabilisons les fonctions choisies par la stratégie et ayant un réel impact sur la résolution. Pour évaluer le bénéfice de chaque méthode nous avons mesuré :

pour CP: le nombre de réductions efficaces effectuées et le nombre de découpages,
et pour AG : le fait que la génération suivante est globalement meilleure que la précédente.

bacp8

bacp10

bacp12

bacpall

Figure 7.6: Évolution de CP vs AG durant le processus d’optimisation

Tout d’abord, les découpages sont limités à 1% du nombre total de fonctions de bases (fonction de réduction) du fait de la complexité spatiale qu’ils génèrent.

En ce qui concerne les problèmes simples (bacp8, bacp10, bacp12), au début, CP représente 70% de l’effort de recherche : la propagation de contrainte restreint l’espace de recherche. Á l’opposé, AG représente autour de 30%. Pendant cette période, trop peu de consistances locales sont atteintes, et AG ne trouve que des solutions dont le coût est supérieur à 21. Puis, à partir de la seconde moitié du processus de recherche, CP et AG convergent en terme d’efficacité : une majorité des sous-GCSP ont atteint la consistance locale et les contraintes ne réduisent plus les domaines. Á la fin, AG représente 70% de l’effort de recherche pour trouver la solution optimale.

Pour ce qui est des stratégies utilisant AG ou CP uniquement, pour cette implémentation, CP n’est pas capable de trouver une solution réalisable en moins de 10 minutes. AG trouve seul la solution optimale, mais 10 fois plus lentement qu’une résolution hybride AG+CP. C’est pourquoi nous n’avons pas inclus ces résultats dans les tables.

Pour le problème avec toutes les périodes réunies (bacpall), AG et CP commence par avoir une efficacité équivalente seulement, tandis que CP apparaît comme stable, une majorité des opérations sont effectuées par le processus génétique. Ceci peut s’expliquer par le fait que, dans ce cas de figure, les contraintes sont trop faibles vis-à-vis du nombre de variables et par là de la taille de l’espace de recherche engendré. Cependant, dans notre système hybride, AG semble être une méthode très efficace même si les opérateurs des contraintes n’ont pas atteint leurs points fixes.

7.4 Conclusion

Le plus intéressant dans une telle hybridation est la complétude de l’association AG+CP, et le rôle joué par AG et CP dans le processus de recherche (voir figures 7.6): AG optimise les solutions (voir figure 7.1) dans un espace de recherche devenant progressivement consistant localement (et ainsi de plus en plus petit) par l’utilisation de la propagation des contraintes et du découpage. De plus, le cadre présenté laisse une grande liberté tant dans le choix des méthodes utilisées que dans les types de problèmes abordés. Nous avons présenté au chapitre 6 un cadre associant recherche locale, propagation de contrainte et découpage. Or nous n’avons pas encore considéré à ce niveau, la possibilité que les algorithmes génétiques puissent utiliser la recherche locale. Nous souhaitons à présent proposer un modèle général capable d’intégrer la recherche locale, les algorithmes génétiques, la propagation de contraintes et le découpage de manière uniforme.

Chapitre 8

Une formulation hybride

des CSP

Dans ce chapitre, un pas de plus est fait pour l’hybridation des méthodes. En effet, le formalisme présenté ici tend à homogénéiser et simplifier toutes les notions vues jusqu’alors. Nous présentons une réunion des concepts de population et d’ensemble de SCSP dans une structure uniforme.

8.1 Introduction

Nous avons présenté au chapitre 5 le cadre proposé par K. Apt. Ce cadre est étendu au chapitre 6 pour y introduire la recherche locale et le découpage des domaines. Puis au chapitre 7, une deuxième grande famille des méthodes incomplètes, celles des algorithmes génétiques est intégrée. Ce chapitre propose maintenant une nouvelle formulation du cadre théorique général pour la résolution des CSP. Cette formulation se trouve dans un contexte d’hybridation entre :

les méthodes à base de propagation et de découpage,
les méthodes centrées sur le cheminement d’une configuration dans l’espace des affectations possibles,
et des algorithmes qui manipulent un ensemble d’individus.

Nous allons donc présenter un cadre de résolution capable d’intégrer ces trois grandes classes de méthodes en un même modèle. La démarche est similaire, elle se base sur une application de fonctions élémentaires sur une structure ordonnée. Dans un premier temps, nous allons construire notre ordre partiel de manière à ce que par la suite, cette structure puisse s’intégrer, dans un second temps, dans un cadre théorique d’application de fonctions. Dans cette partie, nous allons décrire deux fonctions élémentaires : échantillonnage et réduire. Enfin, par les combinaisons de ces deux éléments de base, nous sommes capables de décrire la recherche locale, la propagation de contrainte, le découpage et les algorithmes évolutionnistes.

8.2 Un système hybride pour les CSP

Dans le modèle décrit par K. Apt, la réduction de domaine correspond au calcul de point fixe d’un ensemble de fonctions sur un ordre partiel. Ces fonctions, appelées fonctions de réduction abstraient la notion de contrainte. Nous avons étendu ce cadre pour les algorithmes génétiques et pour la recherche locale. Maintenant, nous proposons ici, une nouvelle formulation d’un cadre uniforme capable de modéliser un algorithme hybride de manière plus simple.

L’idée centrale de ce système est de décomposer le processus de résolution en fonctions de base et d’étendre les travaux de K. Apt à la résolution par les métaheuristiques.

Ces fonctions seront alors gérées au même niveau et la résolution sera réalisée par l’algorithme générique proposé dans [ Apt1997]. Dans notre système, cette résolution se traduit par une séquence de transition sur une structure de calcul.

8.2.1 Construction d’un ordre partiel

Nous utilisons les définitions déjà présentées au chapitre 5.2 concernant l’ordre partiel. Nous rappelons qu’un ordre partiel est un couple (D,\sqsubseteq), avec D un ensemble et \sqsubseteq une relation réflexive, antisymétrique et transitive portant sur D. Considérons un ordre partiel (D,\sqsubseteq), un élément d de D est alors appelé plus petit élément si d \sqsubseteq e pour tous e ∈ D.

De plus, pour un ensemble D, on note P(D) l’ensemble des sous-ensembles possibles de D. (P(D), ⊇ ) forme un ordre partiel, où ⊇ est la relation d’inclusion inverse.

Considérons maintenant le produit cartésien P(D₁) ×... ×P(D_n) dont les éléments sont ordonnés selon la relation d’inclusion inverse ⊇ , telle que : (X₁,...,X_n) ⊇ (Y₁,...,Y_n) ssi X_i ⊇ Y_i pour tout i ∈ [1..n] avec X_i,Y_i ∈ P(D_i). Ceci nous fournit l’ordre partiel : (P(D₁) ×... ×P(D_n), ⊇ )

Pour étendre cette relation aux CSP ; nous construisons un ordre sur ⟨X,C,P(D₁) ×... ×P(D_n)⟩ l’ensemble des CSP avec un ensemble de variables X, un ensemble de contraintes C et un espace de recherche P(D₁) ×... ×P(D_n), équivalent à l’ensemble des CSP possibles depuis le CSP initial ⟨X,C,D₁ ×... ×D_n ⟩ à résoudre.

Le couple (⟨X,C,P(D₁) ×... ×P(D_n) ⟩, \sqsubseteq) forme un ordre partiel, la relation \sqsubseteq étant définie selon la relation inverse ensembliste sur le dernier composant du triplet (correspondant aux domaines).

L’ensemble (⟨X,C,P(D₁) ×... × P(D_n) ⟩ représente celui des CSP possibles. Seulement, gardons à l’esprit que pour une résolution complète il est souvent nécessaire de diviser le problème en sous-problèmes (par découpage d’un domaine ou par énumération des valeurs) et que la résolution se fait dans ce cas, non pas sur un seul, mais sur un ensemble de CSP. Si nous voulons considérer la résolution dans sa totalité, il nous faut alors décrire tous les ensembles possibles de CSP.

Définition 37
Considérons l’ensemble P(P(D₁) ×... ×P(D_n)) des sous-ensembles possibles de P(D₁) ×... ×P(D_n). Considérons la relation \sqsubseteq sur celui-ci définie par :

Étant donné deux ensembles de CSP F et Y membres de l’ensemble P(P(D₁) ×... × P(D_n) avec F = {f₁,...,f_k} et Y = {y₁,...,y_l}. Le couple (F,Y) ∈ \sqsubseteq (i.e. F\sqsubseteq Y) ssi :

∀f_i ∈ F:

(a1) soit il existe y_j ∈ Y t.q. y_j = f_i

(a2) ou soit il existe y_j₁ ..., y_{j_h} ∈ Y t.q. Sol(f_i) ⊆ U_k=1..h Sol(y_{j_k}).

(b) et, ∀y_j ∈ Y ∃f_i ∈ F t.q. f_i \sqsubseteq y_j

La définition de la relation d’ordre sur les ensembles de CSP est primordiale.

Notre objectif sera par la suite d’utiliser cette structure, chaque élément de l’ensemble P(P(D₁)×... ×P(D_n) sera une étape de la résolution. Un élément correspond à un ensemble de CSP, parmi ces CSP certains seront des affectations complètes utiles à la recherche locale ou aux algorithmes génétiques, d’autres seront enclins à une réduction de leurs domaines par les méthodes de filtrage. Mais cet ensemble conservera des propriétés fondamentales quant à la préservation des solutions qui confère à la résolution sa nature complète.

De la définition de cet ordre, nous en déduisons la propriété suivante.

Propriété 3 Cette relation sur les CSP forme un semi-ordre.

Pour prouver que nous sommes face à un semi-ordre, nous allons démontrer que la relation d’ordre est réflexive, que l’antisymétrie n’est pas systématique et qu’elle est transitive.

₁

(a1) Chaque CSP est égal à lui-même ∀f_i ∈ F, f_i = f_i.
(b) Une telle relation n’est pas stricte, chaque CSP est comparable à lui même : ∀f_i, f_i \sqsubseteq f_i

₁

’

₁

_k+1

’

≠

’

Figure 8.1: Démonstration de la transitivité

8.1

(c,a) ∀w_i ∈ W.
- (c,a1) soit il existe y_k ∈ Y t.q. y_k = w_i
- (c,a2) ou soit il existe y_k₁ ..., y_{k_h} ∈ Y t.q. Sol(w_i) ⊆ U_l=1..h Sol(y_{k_l}).
(c,b) et, ∀y_k ∈ Y ∃w_i ∈ W t.q. w_i \sqsubseteq y_k

8.1

∀w_i ∈ W, ∃f_j ∈ F t.q. w_i = f_j

de même concernant le point (a1) de la seconde hypothèse (h2a1)

∀f_j ∈ F, ∃y_k ∈ Y t.q. f_j = y_k

on a alors (c,a1) :

w_i = f_j = y_k
ou (h2a2) seconde hypothèse, ordre sur l’ensemble des solutions, dans ce cas, il existe

y_k₁ ..., y_{k_h} ∈ Y t.q. Sol(f_j) ⊆
∪
l=1..h
Sol(y_{k_l})

, par là (c,a2) :

Sol(w_i) ⊆
∪
l=1..h
Sol(y_{k_l})

f_j₁ ..., f_{j_h} ∈ F t.q. Sol(w_i) ⊆

∪
l=1..h

Sol(f_{j_l})

et (h2a1)

∀f_{j_l} ∃y_{k_l} ∈ Y t.q. f_{j_l} = y_{k_l}

donc (c,a2) :

Sol(w_i) ⊆
∪
l=1..h
Sol(y_{k_l})
ou (h2a2) :

∀f_{j_l} ∃y_{j_l}¹ ..., y_{j_l}^k ∈ Y t.q. Sol(f_{j_l}) ⊆
∪
m=1..k
Sol(y_{j_l}^m)

nous avons (c,a2)

Sol(w_i) ⊆
∪
l=1..h
(
∪
m=1..k
(Sol(y_{j_l}^m)))

∀y_k ∈ Y

∃f_j ∈ F t.q. f_j \sqsubseteq y_k

∈

⟨

₁

⟩

∈

^[¯]

La propriété de quasi-ordre est essentielle, car notre but est d’utiliser cette structure comme support d’application de fonctions monotones et inflationnaires et donc par cette relation d’ordre nous sommes en mesure de montrer la convergence d’un ensemble de fonctions (voir chapitre 5.5).

8.2.2 Fonctions de réduction de domaines

Le calcul du plus petit point fixe commun de l’ensemble de fonctions F peut être réalisé par l’algorithme Générique Itératif de [ Apt2003] décrit par la figure 8.2. Dans cet algorithme, G représente l’ensemble courant des fonctions devant être appliquées (G ⊆ F), d est un élément d’un ensemble partiellement ordonné (les domaines dans le cas des CSP).

GI: Algorithme Générique Itératif
d : = ⊥;
G : = F;
Tant que G ≠ Æ faire
        choisir g ∈ G;
        G : = G - {g};
        G : = G Uactualise(G,g,d);
        d : = g(d);
Fin tant que

Où pour tout G,g,d, l’ensemble des fonctions actualise(G,g,d) de F est tel que :

{ f ∈ F - G | f(d) = d ∧f(g(d)) ≠ g(d)} ⊆ actualise(G,g,d).
g(d) = d implique que actualise(G,g,d) = Æ.
g(g(d)) ≠ g(d) implique que g ∈ actualise(G,g,d)

Figure 8.2: L’algorithme générique itératif

Les propriétés de terminaisons sont identiques à celles présentées au chapitre 5.1. Si toutes nos fonctions sont inflationnaires, monotones et que (D,\sqsubseteq) est fini, alors l’algorithme GI termine et calcul le plus petit point fixe commun des fonctions.

Nous allons voir quelles sont dans notre cas les fonctions en question. Nous proposons un cadre où les fonctions se conforment à deux modèles de fonctions : échantillonnage et réduction.

8.2.3 Échantillonnage

L’échantillonnage, comme nous avons vu au chapitre 6.2, consiste à extraire depuis un CSP une affectation complète ou partielle. L’échantillon est alors ici considéré comme un nouveau CSP ajouté à l’ensemble. Seulement, le fait d’ajouter un CSP à notre ensemble ne remet pas en cause la cohérence de cet ensemble. En effet, aucune solution n’est supprimée et aucune n’est ajoutée puisque l’échantillonnage ne fait qu’extraire une affectation déjà présente dans un autre CSP :

S :

P(⟨X,C,P(D₁) ×...×P(D_n)⟩)

→ P(⟨X,C, P(D₁) ×... ×P(D_n)⟩)

{f₁, ..., f_n }

→ {f₁, ..., f_n,f_n+1}

t.q. ∃f_i avec f_i \sqsubseteq f_n+1

Nous parlerons d’affectation complète si : f_n+1 º ⟨X_n+1;C_n+1;D_n+1⟩ avec D_n+1 = D_n+1₁,...,D_{n+1_k} et ∀i ∈ [1..k], |D_{n+1_i} | = 1 .

Ou partielle si seules certaines variables sont instanciées : f_n+1 º ⟨X_n+1;C_n+1;D_n+1⟩ avec D_n+1 = D_n+1₁,..., D_{n+1_k} et ∃i ∈ [1..k] tq | D_{n+1_i} | = 1

Propriété 4
L’échantillonnage est inflationnaire x \sqsubseteq S(x)
{f₁, ..., f_n } \sqsubseteq {f₁, ..., f_n,f_n+1}, la preuve est directe.
Propriété 5 L’échantillonnage est monotone : x \sqsubseteq y implique S(x) \sqsubseteq S(y) :

F\sqsubseteq Y→ S(F) \sqsubseteq S(Y)

avec

F = {f₁, ..., f_n } et Y = {y₁, ..., y_m}

nous avons :

{f₁, ..., f_n } \sqsubseteq {y₁, ...,y_m} → {f₁, ..., f_n, f_n+1 }\sqsubseteq {y₁, ...,y_m, y_m+1}

Monotonie

∀f_i ∈ F
- ∀f_i ∈ F, i ≠ n+1: d’après l’hypothèse et la définition de l’ordre, les points (a1) ou (a2) sont vérifiés
- f_n+1 par la définition de l’échantillonnage ∃f_i t.q. f_i \sqsubseteq f_n+1.
  Mais d’après la définition de l’ordre pour f_i deux cas, soit :
  (1) ∃y_j ∈ Y t.q. f_i = y_j,
  ou (2) ∃y_j₁, ..., y_{j_h} ∈ Y t.q. Sol_D(f_i) ⊆ U_k=1..h Sol_D(y_{j_k}’).
  
  si nous nous trouvons dans le cas (a1) alors sol(f_n+1) ⊆ sol(y_j) car sol(f_n+1) ⊆ sol(f_i) et sol(f_n+1) = sol(f_i)
  
  si par contre nous sommes dans le cas (a2) alors sol(f_n+1) ⊆ U_k=1..h Sol_D(y_{j_k}) car sol(f_n+1) ⊆ sol(f_i)
∀y_j ∈ Y d’après l’hypothèse, il existe f_i ∈ F t.q. f_i \sqsubseteq y_j
- ∀y_j ∈ Y avec j ≠ m+1 par définition.
- ∃y_l t.q. y_m+1 \sqsubseteq y_l mais ∃i t.q. f_i \sqsubseteqy_j donc f_i \sqsubseteq y_m+1

^[¯]

8.2.4 Réduire

Réduire l’espace de recherche est essentiel pour obtenir une solution par une approche complète, dans le contexte des CSP, cela se traduit par une suppression de valeurs dans les domaines, et ce en étant sûr de ne pas perdre de solutions. Réduire signifie réduire les domaines, mais aussi plus largement, réduire le problème en supprimant les affectations de l’espace de recherche qui ne sont pas solution.

R :

P(⟨X,C,P(D₁) ×...×P(D_n)⟩)

→ P(⟨X,C, P(D₁) ×... ×P(D_n)⟩)

{f₁, ..., f_i, ..., f_n }

→ {f₁, ..., f_i’,..., f_n}

telle que Sol({f₁, ..., f_i, ..., f_n }) = Sol({f₁, ..., f_i’,..., f_n}) et Où f_i’ = Æ ou f = ⟨X,C,D_i ⟩ et f’ = ⟨X,C,D_i’⟩ t.q. D_i’ ⊆ D_i. Ainsi, la fonction réduire R non seulement réduit les domaines, mais aussi supprime des CSP de notre ensemble (f_i’ = Æ). Un CSP est supprimé si par exemple un des domaines des variables est vide, auquel cas ce sous-problème est inconsistant et peut être supprimé sans induire une perte de solutions. Ce CSP supprimé peut aussi être une affectation complète (tous les domaines sont des singletons) et dans la mesure où celle-ci n’est pas solution, il peut être supprimé de l’ensemble.

8.3 Fonction de réduction

Nos deux principes échantillonnage et reduire vont nous permettent de définir un ensemble de fonctions. Nous pouvons dorénavant construire des combinaisons pour décrire à la fois le fonctionnement des méthodes complètes, mais aussi celui des méthodes incomplètes.

8.3.1 La réduction de domaine

La réduction de domaine (DR) correspond à la consistance de n ud, consistance d’arc et la consistance hyper-arc. Le filtrage des valeurs inconsistantes se concrétise par une réduction des domaines et donc entre dans le cadre grâce à la fonction réduire. Á l’aide du schéma de fonction de réduction elle se défini par :

{ f₁, ..., f_i, ..., f_n} →^DR {f₁, ..., f_i’, ..., f_n}

Où DR = R^m avec m > 0.

{ ⟨X,C,D ⟩₁, ..., ⟨X,C,D⟩_i,...,⟨X,C,D ⟩_n }

→^DR { ⟨X,C,D ⟩₁, ..., ⟨X,C,D’⟩_i,...,⟨X,C,D ⟩_n }

où D’ ⊆ D pour le CSP ⟨X,C,D ⟩_i.

Ainsi DR correspond à une ou plusieurs applications de la fonction de base R, ceci pour modéliser le fait que bien souvent, lorsqu’un opérateur spécifique de réduction est défini pour une contrainte, il ne contente pas de réduire un seul domaine. Prenons à titre d’exemple la procédure AllDiff (voir chapitre 2.4.1), pour tout domaine singleton, une réduction des autres domaines est appliquée.

8.3.2 Le découpage

Le découpage (SP) est le résultat du fractionnement d’un domaine, et formellement, pour un domaine de taille m, est vu comme m échantillons générés et par la réduction (suppression) du CSP original tout en conservant les solutions. Le découpage remplace ainsi le problème initial par un ensemble de sous problèmes :

{ f₁, ..., f_i, ..., f_n} →^SP {f₁, ..., f¹_i, ...,f^m_i, ..., f_n}

Où SP = S^mR.

{ ⟨X,C,D ⟩₁, ..., ⟨X,C,D⟩_i,...,⟨X,C,D ⟩_n }

→^SP {⟨X,C,D ⟩₁, ..., ⟨X,C,D⟩_i₁,...,⟨X,C,D ⟩_{i_h},...,⟨X,C,D ⟩_n }

où D₁ = U_{j ∈ [1..h]} D_{i_j}

{⟨X,C,D ⟩₁, ..., ⟨X,C,D⟩_i,...,⟨X,C,D ⟩_n }

→^S{ ⟨X,C,D ⟩₁, ..., ⟨X,C,D⟩_i₁,...,⟨X,C,D ⟩_{i_h},...,⟨X,C,D ⟩_n }

où D₁ = U_{j ∈ [1..h]} D_{i_j}

L’application d’un découpage SP conserve l’ensemble des solutions de par les propriétés de S et R.

8.3.3 La recherche locale

Un chemin de recherche locale (LS) a pour but de générer de nouveaux échantillons et de se déplacer vers un voisin choisi. De manière formelle cela correspond à m échantillonnage (générer le voisinage) suivi de m réduction (choisir le voisin).

{ f₁, ..., f_i, ..., f_n} →^LS {f₁, ..., f_i’, ..., f_n}

Où LS = S^mR^m-1.

{ ⟨X,C,D₁ ⟩₁, ..., ⟨X,C,D_i ⟩_i,...,⟨X,C,D_n ⟩_n }

→^LS { ⟨X,C,D₁ ⟩₁, ..., ⟨X,C,D’_i ⟩_i,...,⟨X,C,D_n ⟩_n }

où il existe ⟨X,C,D_j ⟩ t.q. D’_i ⊂ D_j

Cette combinaison modélise bien la recherche locale puisque dans une recherche locale (voir chapitre 3), un certain nombre de voisins sont générés autour de la configuration courante, puis parmi ces voisins un seul est choisi, les autres sont supprimés et une trace de la recherche est conservée (m-1).

8.3.4 L’évolution

Pour décrire les algorithmes génétiques avec nos deux éléments de base que sont R et S, nous devons décrire tous les opérateurs génétiques de manière indépendante. L’évolution peut se diviser en trois mouvements : le croisement CR correspond à un échantillonnage, la mutation MU, elle, est un échantillonnage suivi d’une réduction quant à la sélection SE (d’une sous-population). Elle équivaut à un nombre s de réductions. La construction d’un algorithme génétique spécifique se fait alors par l’utilisation de ces trois fonctions.

{ f₁, ..., f_n} →^CR {f₁, ..., f_n,f_n+1 }

où CR = S.

{ f₁, ..., f_i, ..., f_n} →^MU {f₁, ..., f_i’, ..., f_n }

où MU = SR.

{ f₁, ..., f_n} →^SE {f₁, ..., f_n’}

où SE = R^s.

Ainsi, une résolution est une séquence finie depuis le problème initial ⟨X,C,D₀ ⟩ et produit en état final ⟨X,C,D¹_n ⟩,..., ⟨X,C,D^k_n ⟩ par application des règles de transition présentées précédemment.

Dans ce contexte, une stratégie est une séquence (t_i)_{1 ≤ i ≤ n} où ∀1 ≤ i ≤ n, t_i ∈ {DR,SP,LS,SE,CR,MU}. Or chaque élément de cet ensemble correspond en réalité à une combinaison des fonctions S et R. Ce qui finalement, au niveau le plus bas, est fourni à l’algorithme générique itératif ce sont ces deux fonctions monotones et inflationnaires.

8.4 Conclusion

Les techniques hybrides nous permettent d’atteindre un degré élevé d’efficacité pour résoudre des problèmes combinatoires et d’optimisation complexes. Dans ce chapitre, nous présentons un cadre général approprié pour modéliser la résolution par l’algorithme hybride. Nous avons montré que ce travail peut servir de base pour la formulation d’une intégration des algorithmes génétiques, de la recherche locale et de la programmation par contraintes avec leurs principales propriétés.

Ce cadre fournira un environnement uniforme pour classifier, comparer, analyser, décrire et contrôler des algorithmes hybrides au niveau le plus basique.

Conclusion Générale

Principales contributions

Cette thèse s’articule autour d’une modélisation des mécanismes de résolution des problèmes de satisfaction de contraintes.

Nous avons proposé dans un premier temps une intégration de la recherche locale au sein d’un cadre préexistant, initialement conçu pour décrire la propagation de contrainte. Ce cadre est alors étendu pour considérer d’une part le découpage des domaines et d’autre part les mécanismes inhérents à la résolution par les méthodes de recherche locale. Ce cadre repose sur un nouveau modèle, celui de CSP échantillonné. Nous avons alors confronté ce modèle à diverses expérimentations dans lesquelles une résolution hybride s’avère efficace pour résoudre des problèmes de satisfaction de contraintes classiques. L’homogénéisation des concepts de résolution, nous a permis de nous dégager d’une hiérarchie, processus maître processus esclave, pour modéliser des algorithmes de résolution hybride.

Dans un second temps, nous avons envisagé une fusion des méthodes complètes avec les algorithmes génétiques. Cette association a permis en outre, la résolution d’un problème d’optimisation sous contraintes. Nous avons corollairement identifié les interactions entre l’évolution d’une population et la réduction de l’espace de recherche dont elle est issue. Nous avons souligné par des expérimentations la complémentarité de ces méthodes.

Cette étude des différentes hybridations entre les méthodes complètes et incomplètes a nécessité une part non négligeable de développement. En effet, nous avons développé notre propre solveur de manière à bien étudier les comportements des méthodes au plus bas niveau. Ce solveur a évolué au même titre que les niveaux d’hybridations jusqu’à la résolution des problèmes d’optimisation sous contraintes.

Enfin, nous avons montré que ce travail peut servir de base pour une intégration des méthodes de recherche locale, des algorithmes génétiques et de la programmation par contraintes dans le but de préciser les connexions entre des techniques incomplètes et complètes et d’en extraire les principales propriétés. Nous avons montré de même que l’intégration de ces techniques peut se faire dans le cadre des itérations chaotiques. Cependant, une nouvelle structure ordonnée de calculs est alors requise ainsi que des fonctions de réductions adaptées.

Les frontières existantes entre les méthodes complètes et incomplètes, même si elles existent toujours, peuvent être atténuées dans notre approche, quand il s’agit de fournir des preuves sur la correction, la complétude et la fiabilité des méthodes hybrides.

Perspectives de recherches

Dans un futur proche, nous envisageons le développement de notre solveur vers une librairie C++ capable de calquer le modèle théorique pour offrir aux utilisateurs la possibilité de tester et d’imaginer une gamme très large de combinaisons de ces méthodes.

Il nous reste beaucoup d’extensions du modèle à explorer, nous projetons notamment une adaptation de la méthode Go With the Winners [ Aldous and Vazirani1994] aux arbres de recherche des méthodes hybrides. Ceci peut passer par une distribution de la recherche en différents points et par une communication via les particules échangées.

Nous souhaitons aussi développer des outils d’apprentissage capables de nous soustraire aux difficultés liées à la définition des paramètres et plus généralement, aux stratégies.

Il est sans doute encore utopique d’envisager un système intelligent capable de s’adapter à toute sorte de problèmes, d’en déduire la stratégie optimale de résolution et de l’expliquer à l’utilisateur.

Liste des figures

List of Figures

    1.1 Exemple de problème de coloriage de carte et son équivalent en problème de satisfaction de contraintes
    1.2 Une solution pour le placement de 8 reines sur un échiquier
    1.3 Solution d’une règle de Golomb à 4 marques
    1.4 Carré magique d’ordre 4
    1.5 Quels sont les chiffres associés aux lettres S E N D M O R Y?
    1.6 Solution du nombre de Langford (2,4)
    1.7 Solution du nombre de Langford (3,9)
    1.8 Pouvons nous trouver un chemin qui partant de x₂ qui passe par tous les sommets et ce pour un coût inférieur 40 : La solution x₂, x₄, x₆, x₅, x₃, x₄, x₁ semble adéquate.
    2.1 Arbre de recherche du backtracking
    2.2 CSP non consistant
    2.3 Applications successives de la procédure Révise_arc
    2.4 Arbre de recherche : propagation + énumération
    2.5 Arbre de recherche du Forward Checking
    2.6 Arbre de recherche du Full Look Ahead
    3.1 Chemin de recherche locale
    3.2 Minimum local et global
    3.3 Minimum local et Recuit Simulé
    3.4 Diversification avec une liste tabou
    3.5 Exemple de croisement uniforme
    3.6 Exemple de mutation sur un gène
    3.7 Exemple de sélections
    3.8 Mécanisme général des algorithmes génétiques.
    4.1 Classification des combinaisons exactes/métaheuristiques
    4.2 Processus de recherche LDS
    5.1 Modèle abstrait
    5.2 Exemple d’ordre partiel
    6.1 Processus hybride de résolution sur un ordre partiel
    6.2 Fonction de sélection
    6.3 Interaction entre voisinage et espace réduit
    6.4 Exemple de grille de Sudoku
    6.5 Coût d’une solution : nombre de Langford (Depth-First)
    6.6 Coût d’une solution : Send+More=Money (Depth-First)
    7.1 Algorithme génétique pour l’optimisation
    7.2 Schéma général d’application des fonctions pour l’hybridation CP+GA
    7.3 Exemple de distribution des cours.
    7.4 fonctions ga
    7.5 Évolution des fonctions de coût
    7.6 Évolution de CP vs AG durant le processus d’optimisation
    8.1 Démonstration de la transitivité
    8.2 L’algorithme générique itératif

Listes des tables

List of Tables

    6.1 Résultats du Sudoku par différentes méthodes de recherche
    6.2 Meilleures gammes du taux de propagation pour calculer une solution
    6.3 Nombre moyen d’opérations pour calculer une première solution
    7.1 Résultats en seconde avec lp_solve
    7.2 Résultats avec GA+CP

Listes des algorithmes

Liste des publications personnelles

Conférences internationales avec comité de sélection

Tony Lambert, Carlos Castro, Eric Monfroy et Frédéric Saubion. Solving the Balanced Academic Curriculum Problem with an Hybridization of Genetic Algorithm and Constraint Propagation. International Conference on Artificial Intelligence and Soft Computing (ICAISC’06). pp 410-419, Volume 4029 of Lecture Notes in Artificial Intelligence, Zakopane, Poland, Springer Verlag 2006.
Tony Lambert, Eric Monfroy et Frédéric Saubion. Solving Sudoku with Local Search : A Generic Framework. International Conference on Computational Science (ICCS 2006), pp 641-648, Volume 3991 of Lecture Notes in Computer Science, May 28-31, Reading, UK, Springer Verla 2006.
Eric Monfroy, Frédéric Saubion et Tony Lambert. Hybrid CSP Solving, Proceeding of 5th International Workshop Frontiers of Combining Systems (FroCoS), pp 138-167, Bernhard Gramlich, Volume 3717 of Lecture Notes in Computer Science, Vienna, Austria, September 19-21, Springer 2005, invited paper.
Tony Lambert, Carlos Castro, Eric Monfroy, María Cristina Riff et Frédéric Saubion. Hybridization of Genetic Algorithms and Constraint Propagation for the BACP, Logic Programming, 21st International Conference, ICLP 2005, pp 421-423, Volume 3668 of Lecture Notes in Computer Science, spain, October 2 - 5, M. Gabbrielli and G. Gupta, Springer, 2005.
Tony Lambert, Eric Monfroy et Frédéric Saubion. Solving Strategies using a Hybridization Model for Local Search and Constraint Propagation. Proceedings of the 2005 ACM Symposium on Applied Computing (SAC), Santa Fe, New Mexico, USA. pages 398-403, Hisham Haddad and Lorie M. Liebrock and Andrea Omicini and Roger L. Wainwright, Santa Fe, New Mexico, USA, March 13-17, ACM, 2005.
Eric Monfroy, Frédéric Saubion et Tony Lambert. On Hybridization of Local Search and Constraint Propagation, Logic Programming, 20th International Conference, ICLP 2004, pages = 299-313, Volume 3132 of Lecture Notes in Computer Science, Bart Demoen and Vladimir Lifschitz, Saint-Malo, France, September 6-10, Springer Verlag, 2004.

Ateliers internationaux avec comité de sélection

Tony Lambert, Carlos Castro, Eric Monfroy, María Cristina Riff et Frédéric Saubion. Hybridization of Genetic Algorithms and Constraint Propagation : application to the Balanced Academic Curriculum Problem, In Proceeding of the 5th Workshop on Cooperative Solvers in Constraint Programming (COSOLV), Sitges, Spain, October, 2005.
Tony Lambert, Eric Monfroy et Frédéric Saubion. Hybridization Strategies for Local Search and Constraint Propagation, Proceeding of the 4th Workshop on Cooperative Solvers in Constraint Programming (COSOLV), Toronto, Canada, September, 2004.

Conférences nationales avec comité de sélection

Tony Lambert, Carlos Castro, Eric Monfroy, María Cristina Riff et Frédéric Saubion. Résolution du problème d’équilibrage des diplômes grâce à l’hybridation d’algorithmes génétiques et de la propagation de contraintes, Actes des 1ères Journées Francophones de Programmation par Contraintes (JFPC’2005),pp 423-426, C. Solnon, 2005.
Hervé Deleau, Tony Lambert, Eric Monfroy et Frédéric Saubion. Iterations chaotiques pour l’hybridation propagation de contraintes/recherche locale, Programmation en logique avec contraintes, JFPLC 2004, Frédéric Mesnard, pp 221-237, 21, 22 et 23 Juin, Angers, France, Hermès, 2004.

Références bibliographiques

[ Aarts and Lenstra1997]: E. Aarts and J.K. Lenstra, editors. Local Search in Combinatorial Optimization. John Wiley and Sons, 1997.
[ Aggoun and Beldiceanu1991]: A. Aggoun and N. Beldiceanu. Overview of the chip compiler system. In K. Furukawa, editor, Logic Programming, Proceedings of the Eigth International Conference, pages 775-789. MIT Press, 1991.
[ Ahuja et al. 2002]: R. K. Ahuja, Ö. Ergun, J. B. Orlin, and A. P. Punnen. A survey of very large-scale neighborhood search techniques. Discrete Appl. Math., 123(1-3):75-102, 2002.
[ Aldous and Vazirani1994]: D.J. Aldous and U. Vazirani. Go with the winners algorithms. In Proc. 35th Symp. Foundations of Computer Sci., pages 492-501. IEEE Computer Soc. Press, 1994.
[ Allen1983]: J. F. Allen. Maintaining knowledge about temporal intervals. Commun. ACM, 26(11):832-843, 1983.
[ Allen1984]: J. F. Allen. Towards a general theory of action and time. Artif. Intell., 23(2):123-154, 1984.
[ Applegate et al. 1998]: D. Applegate, R. Bixby, V. Chvátal, and W. Cook. On the solution of traveling salesman problems. Documenta Mathematica, Extra Volume Proceedings ICM III (1998):645-656, 1998.
[ Apt1997]: K. Apt. From chaotic iteration to constraint propagation. In 24th International Colloquium on Automata, Languages and Programming (ICALP ’97), number 1256 in LNCS, pages 36-55. Springer, 1997. invited lecture.
[ Apt1999]: K. Apt. The rough guide to constraint propagation. In Springer-Verlag, editor, Proc. of the 5th International Conference on Principles and Practice of Constraint Programming (CP’99), volume 1713 of LNCS, pages 1-23, 1999. (Invited lecture).
[ Apt2003]: K. Apt. Principles of Constraint Programming. Cambridge University Press, 2003.
[ Bäck et al. 2001]: T. Bäck, J. M. de Graaf, J. N. Kok, and W. A. Kosters. Theory of genetic algorithms. In Gheorghe Paun, Grzegorz Rozenberg, and Arto Salomaa, editors, Current Trends in Theoretical Computer Science, Entering the 21th Century, pages 546-578. World Scientific, 2001.
[ Baker1985]: J. E. Baker. Adaptive selection methods for genetic algorithms. In ICGA, pages 101-111, 1985.
[ Benhamou1996]: F. Benhamou. Heterogeneous constraint solving. In M. Hanus and M. Rodriguez Artalejo, editors, Proceedings of the Fifth international conference on algebraic and logic programming, ALP’96, number 1139 in LNCS. Springer-Verlag, 1996.
[ Bessière and Régin2001]: C. Bessière and J.C. Régin. Refining the basic constraint propagation algorithm. pages 309-315, 2001.
[ Bessière et al. 1999]: C. Bessière, E.C. Freuder, and J.C. Régin. Using constraint metaknowledge to reduce arc consistency computation. AAAI, pages 125-148, 1999.
[ Bessière1994]: C. Bessière. Arc-consistency and arc-consistency again. Artificial Intelligence, pages 179-190, 1994.
[ Bruynooghe1985]: M. Bruynooghe. Graph coloring and constraint satisfaction. Technical Report CW 44, Katholieke Universiteit Leuven, 1985.
[ Burke et al. 2001]: E. K. Burke, P. I. Cowling, and R. Keuthen. Effective local and guided variable neighbourhood search methods for the asymmetric travelling salesman problem. In Proceedings of the EvoWorkshops on Applications of Evolutionary Computing, pages 203-212, London, UK, 2001. Springer-Verlag.
[ Castro and Manzano2001]: C. Castro and S. Manzano. Variable and value ordering when solving balanced academic curriculum problems. In Proceedings of 6th Workshop of the ERCIM WG on Constraints. CoRR cs.PL/0110007, 2001.
[ Chakravarthy1979]: I. Chakravarthy. A generalized line and junction labeling scheme with applications to scene analysis. IEEE Trans. Pattern Analysis and Machine Intelligence, vol. 1, pages 202-205, 1979.
[ Chazan and Miranker1969]: D. Chazan and W. L. Miranker. Chaotic relaxation. Linear algebra and its applications, 2:199-222, 1969.
[ Colmerauer1990]: A. Colmerauer. An introduction to prolog iii. CACM, 33(7):69-90, Jul 1990.
[ Colmerauer1994]: A. Colmerauer. Spécifications de prolog iv. Tech. rept., GIA, Faculté des Sciences de Luminy, Marseille, France, 1994.
[ Congram2000]: R. K. Congram. Polynomially Searchable Exponential Neighbourhoods for Sequencing Problems in Combinatorial Optimisation. Phd thesis, University of Southampton, Faculty of Mathematical Studies, UK, 2000.
[ Cooper1989]: M. C. Cooper. An optimal k-consistency algorithm. Artif. Intell., 41(1):89-95, 1989.
[ Cotta and Troya2003]: C. Cotta and J. M. Troya. Embedding branch and bound within evolutionary algorithms. Appl. Intell., 18(2):137-153, 2003.
[ Cousot and Cousot1977]: P. Cousot and R. Cousot. Automatic synthesis of optimal invariant assertions: mathematical foundations. In ACM Symposium on Artificial Intelligence & Programming Languages, Rochester, NY, ACM SIGPLAN Not. 12(8):1-12, August 1977.
[ Cousot1978]: P. Cousot. Méthodes itératives de construction et d’approximation de points fixes d’opérateurs monotones sur un treillis, analyse sémantique de programmes. Thèse d’état en sciences mathématiques, Université scientifique et medicale de Grenoble, France, 1978.
[ Croker and Dhar1993]: A. E. Croker and V. Dhar. A knowledge representation for constraint satisfaction problems. IEEE Transactions on Knowledge and Data Engineering, 5(5):740-752, 1993.
[ Davis and Rosenfeld1981]: L. S. Davis and A. Rosenfeld. Cooperating processes for low-level vision: A survey. Artificial Intelligence, 17(1-3):245-263, août 1981.
[ de Kleer and Syssman1980]: J. de Kleer and G. J. Syssman. Propagation of constraints applied to circuit synthesis. Circuit Theory and Applications, 8:127-144, 1980.
[ Dechter and Dechter1988]: R. Dechter and A. Dechter. Belief maintenance in dynamic constraint networks. Proceedings of the Seventh National Conference on Artificial Intelligence, pages 37-42, 1988.
[ Dechter and Meiri1989]: R. Dechter and I. Meiri. Experimental evaluation of preprocessing techniques in constraint satisfaction problems. In Proc. of the 11th IJCAI, pages 271-277, Detroit, MI, 1989.
[ Dechter et al. 1991]: R. Dechter, I. Meiri, and J. Pearl. Temporal constraint networks. Artif. Intell., 49(1-3):61-95, 1991.
[ Dechter1987]: R. Dechter. A constraint-network approach to truth-maintenance. Technical Report Technical Report 870009 (R-80), UCLA Cognitive Systems Laboratory, 1987.
[ Dechter2003]: Rina Dechter. Constraint Processing. Morgan Kaufmann, May 2003.
[ Deleau2005]: H. Deleau. Approches hybrides pour les problèmes CSP. PhD thesis, Université d’Angers, PhD thesis, 2005.
[ Dhar and Ranganathan1990]: V. Dhar and N. Ranganathan. Integer programming vs. expert systems: an experimental comparison. Commun. ACM, 33(3):323-336, 1990.
[ Eastman1972]: C. M. Eastman. Preliminary report on a system for general space planning. Commun. ACM, 15(2):76-87, 1972.
[ Eiben et al. 1994]: A. E. Eiben, P.-E. Raué, and Z. Ruttkay. Genetic algorithms with multi-parent recombination. In PPSN III: Proceedings of the International Conference on Evolutionary Computation. The Third Conference on Parallel Problem Solving from Nature, volume 866 of Lecture Notes in Computer Science, pages 78-87. Springer, 1994.
[ Fages et al. 1998]: F. Fages, J. Fowler, and T. Sola. Experiments in reactive constraint logic programming. Journal of Logic Programming, 37(1-3):185-212, 1998.
[ Fages1996]: F. Fages. Programmation Logique par Contraintes. Ellipse, 1996.
[ Feltl and Raidl2004]: H. Feltl and G. R. Raidl. An improved hybrid genetic algorithm for the generalized assignment problem. In Hisham Haddad, Andrea Omicini, Roger L. Wainwright, and Lorie M. Liebrock, editors, in Proc. the 2004 ACM Symposium on Applied Computing (SAC), Nicosia, Cyprus, March 14-17, pages 990-995. ACM, 2004.
[ Feo and Resende1995]: T. A. Feo and M. G. C. Resende. Greedy randomized adaptive search procedures. Journal of Global Optimization, 6:109-133, 1995.
[ Fikes1970]: R. Fikes. Ref-arf: A system for solving problems stated as procedures. Artifical Intelligence, 1(1):27-120, 1970.
[ Focacci et al. 2002]: F. Focacci, F. Laburthe, and A. Lodi. Local search and constraint programming. In Fred Glover and Gary Kochenberger, editors, Handbook of Metaheuristics. Kluwer, 2002.
[ Fox et al. 1989]: M. S. Fox, N. Sadeh, and C. Baykan. Constrained heuristic search. In Proceedings of the Eleventh International Joint Conference on Artificial Intelligence, pages 309-315, Detroit, MI, August 1989.
[ Fox1987]: M. S. Fox. Constraint-directed Search: A Case Study of Job-Shop Scheduling. Morgan Kaufmann Publishers, 1987.
[ Frayman and Mittal1987]: F. Frayman and S. Mittal. Cossack : A constraints-based expert system for configuration tasks. Knowledge-Based Expert Systems in Engineering: Planning and Design, pages 143-166, 1987.
[ Fruewirth and Abdennadher2003]: T. Fruewirth and S. Abdennadher. Essentials of Constraint Programming. Springer, 2003.
[ Garey and Johnson1978]: Michael R. Garey and David S. Johnson. Computers and Intractability , A Guide to the Theory of NP-Completeness. W.H. Freeman & Company, San Francisco, 1978.
[ Gaspero and Schaerf2003]: L. Di Gaspero and A. Schaerf. Easylocal++: an object-oriented framework for the flexible design of local-search algorithms. Softw. Pract. Exper., 33(8):733-765, 2003.
[ Geffner and Pearl1987]: H. Geffner and J. Pearl. An improved constraint-propagation algorithm for diagnosis. In Proc. of the 10th IJCAI, pages 1105-1111, Milan, Italy, 1987.
[ Gent et al. ]: I. Gent, T. Walsh, and B. Selman. http://www.4c.ucc.ie/ tw/csplib/, funded by the UK Network of Constraints.
[ Ginsberg and Harvey1990]: M. L. Ginsberg and W. D. Harvey. Iterative broadening. In Proceedings of AAAI-91, 1990.
[ Glover and Laguna1997]: F. Glover and M. Laguna. Tabu Search. Kluwer Academic Publishers, 1997.
[ Glover1977]: F. Glover. Heuristics for integer programming using surrogate constraints. Decision Sciences, 8(1):156-166, 1977.
[ Glover1986]: F. Glover. Future paths for integer programming and links to artificial intelligence. Computers and Operations Research, 13:533-549, 1986.
[ Goldberg1989a]: D. E. Goldberg. Genetic Algorithms in Search, Optimization and Machine Learning. Addison-Wesley Longman Publishing Co, Inc, 1989.
[ Goldberg1989b]: D.E. Goldberg. Genetic Algorithms for Search, Optimization, and Machine Learning. Reading, MA:Addison-Wesley, 1989.
[ Gusgen and Hertzberg1988]: H. W. Gusgen and J. Hertzberg. Some fundamental properties of local constraint propagation. Artif. Intell., 36(2):237-247, 1988.
[ Hao et al. 1999]: J. K. Hao, P. Galinier, and M. Habib. Metaheuristiques pour l’optimisation combinatoire et l’affectation sous contraintes. Revue d’Intelligence Artificielle, 13, 1999.
[ Haralick and Elliott1980]: R. M. Haralick and G. L. Elliott. Increasing tree search efficiency for constraint satisfaction problems. Artif. Intell., 14(3):263-313, 1980.
[ Haralick et al. 1978]: R. M. Haralick, L. S. Davis, A. Rosenfeld, and D. L. Milgram. Reduction operations for constraint satisfaction. Information Science, 14(3):199-219, 1978.
[ Harvey and Ginsberg1995]: W. D. Harvey and M. L. Ginsberg. Limited discrepancy search. In Proc. of the 14th IJCAI, pages 607-613, Montreal, Canada, 1995.
[ Holland1975a]: J. H. Holland. Adaptation in Natural and Artificial Systems. University of Michigan Press, 1975.
[ Holland1975b]: J.H. Holland. Adaptation in Natural and Artificial Systems. University of Michigan Press, 1975.
[ ILOG2000]: ILOG. ILOG Solver 5.0:Reference Manual. ILOG S.A., Gentilly, France, 2000.
[ Jaffar and Lassez1987]: J. Jaffar and J.-L. Lassez. Constraint logic programming. In POPL ’87: Proceedings of the 14th ACM SIGACT-SIGPLAN symposium on Principles of programming languages, pages 111-119, New York, NY, USA, 1987. ACM Press.
[ Jussien and Lhomme2002]: N. Jussien and O. Lhomme. Local search with constraint propagation and conflict-based heuristics. Artificial Intelligence, 139(1):21-45, 2002.
[ Kirkpatrick et al. 1983]: S. Kirkpatrick, C. D. Gelatt, and M. P. Vecchi. Optimization by simulated annealing. Science, Number 4598, 13 May 1983, 220, 4598:671-680, 1983.
[ Klau et al. 2004]: G. Klau, I. Ljubi\’c, A. Moser, P. Mutzel, P. Neuner, U. Pferschy, and R. Weiskircher. Combining a memetic algorithm with integer programming to solve the prize-collecting steiner tree problem. In K. Deb, editor, Genetic and Evolutionary Computation - GECCO-2004, Part I, volume 3102 of Lecture Notes in Computer Science, pages 1304-1315, Seattle, WA, USA, 26-30 June 2004. Springer-Verlag.
[ Krajecki et al. 2005]: M. Krajecki, O. Flauzac, Ch. Jaillet, P.-P. Mérel, and R. Tremblay. Solving an open Instance of the Langford Problem using CONFIIT: a Middleware for Peer-to-Peer Computing. Parallel Processing Letters, 2005.
[ Kumar1992]: V. Kumar. Algorithms for constraint-satisfaction problems: A survey. AI Magazine, 13(1):32-44, 1992.
[ Laburthe and Caseau2002]: F. Laburthe and Y. Caseau. Salsa: A language for search algorithms. Constraints, 7(3-4):255-288, 2002.
[ Laburthe2000]: F. Laburthe. CHOCO: implementing a cp kernel. In CP’00 Post Conference Workshop on Techniques for Implementing Constraint Programming Systems - TRICS, 2000.
[ Lardeux et al. 2005]: Frédéric Lardeux, Frédéric Saubion, and Jin-Kao Hao. Three truth values for the sat and max-sat problems. In Proc. of the Nineteenth International Joint Conference on Artificial Intelligence (IJCAI’05), Lecture Notes in Computer Science, Edinburgh, Scotland, aug 2005. Springer.
[ Mackworth1977]: A.K. Mackworth. Consistency in networks of relations. Artificial Intelligence, 8, 1977.
[ Mackworth1992]: A. K. Mackworth. Constraint satisfaction. In S.C. Shapiro, editor, Encyclopedia of Artificial Intelligence, volume 1, pages 285-293. Wiley Interscience, New York, 1992.
[ Madeline2002]: B. Madeline. Algorithmes évolutionnaires et résolution de problèmes de satisfaction de contraintes en domaines finis. Thèse de doctorat, Université de Nice, Sophia Antipolis, Décembre 2002. Projet COPRIN.
[ Marino et al. 1999]: A. Marino, A. Prugel-Bennett, and C. Glass. Improving graph colouring with linear programming and genetic algorithms. In Proceedings of EUROGEN99, Jyvaskyla, Finland, pp. 113-118., 1999.
[ Mariott and Stuckey1998]: K. Mariott and P. Stuckey. Programming with Constraints, An introduction. MIT Press, 1998.
[ McGregor1979]: J. J. McGregor. Relational consistency algorithms and their application in finding subgraph and graph isomorphisms. Information Sciences, 19:229-250, 1979.
[ Meyer and Jaumard2006]: C. Meyer and B. Jaumard. Equivalence of some lp-based lower bounds for the golomb ruler problem. Discrete Applied Mathematics, 154(1):120-144, 2006.
[ Michalewicz1996]: Z. Michalewicz. Genetic Algorithms + Data Structures = Evolution Programs. Springer Verlag, 1996.
[ Michel and Hentenryck1997]: Laurent Michel and Pascal Van Hentenryck. Localizer: A modeling language for local search. In Proc. of the 1997 International Conference on Constraint Programming, 1997.
[ Mladenovi\’c and Hansen1997]: N. Mladenovi\’c and P. Hansen. Variable Neighborhood Search. Computers and Operations Research, 24(11):1097-1100, 1997.
[ Mohr and Henderson1986]: R. Mohr and T.C. Henderson. Arc and path consistency revisited. Artificial Intelligence, 28:225-233, 1986.
[ Nadel1988]: B. A. Nadel. Tree search and arc consistency in constraint satisfaction algorithms. Search in Artificial Intelligence, pages 287-342, 1988.
[ Nadel1990]: B. A. Nadel. Some applications of the constraint satisfaction problem. In In AAAI-90 Workshop on Constraint Directed Reasoning Working Notes, Boston, Mass., 1990.
[ Nagar et al. 1995]: A. Nagar, S. S. Heragu, and J. Haddock. A combined branch-and-bound and genetic algorithm based approach for a flowshop scheduling problem. Annals of Operations Research, Volume 63, Number 3:397 - 414, 1995.
[ Navinchandra1991]: D. Navinchandra. Exploration and innovation in design: towards a computational model. Springer-Verlag New York, Inc., New York, NY, USA, 1991.
[ Neveu et al. 2004]: B. Neveu, G. Trombettoni, and F. Glover. Idwalk : A candidate list strategy with a simple diversification device. In Principles and Practice of Constraint Programming, CP’04, LNCS. Springer, 2004.
[ Papadimitriou1994]: C. H. Papadimitriou. Computational Complexity. Addison-Wesley Publishing Company, 1994.
[ Pesant and Gendreau1996]: G. Pesant and M. Gendreau. A view of local search in constraint programming. In E. Freuder, editor, Proceedings of the Second International Conference on Principles and Practice of Constraint Programming, number 1118 in LNCS, pages 353-366. Springer, 1996.
[ Petrie et al. 1989]: C. Petrie, R. Causey, D. Steiner, and V. Dhar. A planning problem: Revisable academic course scheduling. Technical Report Technical Report AI-020-89, MCC, Austin,TX, 1989.
[ Prestwich2000]: S. Prestwich. A hybrid search architecture applied to hard random 3-sat and low-autocorrelation binary sequences. In R. Dechter, editor, Principles and Practice of Constraint Programming - CP 2000, number 1894 in LNCS, pages 337-352. Springer, 2000.
[ Prosser1989]: P. Prosser. A reactive scheduling agent. In Proc. of the 11th IJCAI, pages 1004-1009, Detroit, MI, 1989.
[ Puchinger et al. 2004]: J. Puchinger, G. R. Raidl, and G. Koller. Solving a real-world glass cutting problem. In Jens Gottlieb and Günther R. Raidl, editors, Evolutionary Computation in Combinatorial Optimization - EvoCOP 2004, volume 3004 of LNCS, pages 165-176, Coimbra, Portugal, 5-7 April 2004. Springer Verlag.
[ Régin1994]: J. C. Régin. A filtering algorithm for constraints of difference in csps. In AAAI ’94: Proceedings of the twelfth national conference on Artificial intelligence (vol. 1), pages 362-367, Menlo Park, CA, USA, 1994. American Association for Artificial Intelligence.
[ Riff Rojas1996]: M. C. Riff Rojas. From quasi-solutions to solution: An evolutionary algorithm to solve csp. In Proceedings of the Second International Conference on Principles and Practice of Constraint Programming, Cambridge, Massachusetts, USA, August 19-22, volume 1118 of Lecture Notes in Computer Science, pages 367-381. Springer, 1996.
[ Rit1986]: J. F. Rit. Propagating temporal constraints for scheduling. In Proceedings of AAAI-86, Philadelphia, Pa., pages 383-388. AAAI, August 1986.
[ Shaw1998]: P. Shaw. Using constraint programming and local search methods to solve vehicle routing problems. In M. Maher and J.F. Puget, editors, Principles and Practice of Constraint Programming - CP98, 4th International Conference, number 1520 in LNCS, pages 417-431. Springer, 1998.
[ Stefik1981]: M. J. Stefik. Planning with constraints (molgen part 1). Artificial Intelligence, 16(2):111-140, 1981.
[ Tam and Stuckey1999]: V. Tam and P.J. Stuckey. Improving evolutionary algorithms for efficient constraint satisfaction. The International Journal on Artificial Intelligence Tools, 2(8), 1999.
[ Thierens and Goldberg1994]: D. Thierens and D. E. Goldberg. Convergence models of genetic algorithm selection schemes. In PPSN III: Proceedings of the International Conference on Evolutionary Computation. The Third Conference on Parallel Problem Solving from Nature, volume 866 of Lecture Notes in Computer Science, pages 119-129. Springer, 1994.
[ Tsang1987]: E. P. K. Tsang. The consistent labeling problem in temporal reasoning. In Proceedings of the 6th National Conference on Artificial Intelligence, AAAI’87, pages 251-255, 1987.
[ Tsang1993]: E. P. K Tsang. Foundations of Constraint Satisfaction. Academic Press, London, 1993.
[ Ullmann1976]: J. R. Ullmann. An algorithm for subgraph isomorphism. J. ACM, 23(1):31-42, 1976.
[ van Hentenryck and Michel2005]: P. van Hentenryck and L. Michel. Constraint-based local search. Cambridge, Mass. [u.a.] : MIT Press, 2005.
[ van Hentenryck1989]: P. van Hentenryck. Constraint Satisfaction in Logic Programming. MIT Press, 1989.
[ Vasquez and Dupont2002]: M. Vasquez and A. Dupont. Filtrage par arc-consistance et recherche tabou pour l’allocation de fréquence avec polarisation. In Actes des JNPC 2002, 2002.
[ Vilain and Kautz1986]: M. Vilain and H. Kautz. Constraint propagation algorithms for temporal reasoning. In Proceedings of AAAI-86, Philadelphia, Pa., pages 377-382. AAAI, August 1986.
[ Waltz1975]: D.L. Waltz. The Psychology of Computer Vision, chapter Generating Semantic Descriptions from Drawings of Scenes with Shadows. Mc Graw Hill, 1975.
[ Woodruff1999]: D. L. Woodruff. A chunking based selection strategy for integrating meta-heuristics with branch and bound. In Metaheuristics: Advances and Trends in Local Search Paradigms for Optimization, pages 499-511. Kluwer Academic Publishers, 1999.
[ Yato and Seta2002]: T. Yato and T. Seta. Complexity and Completeness of Finding Another Solution and its Application to Puzzles. In Proc. of the National Meeting of the Information Processing Society of Japan IPSJ SIG Notes 2002-AL-87-2, 2002.

Hybridation de méthodes complètes et incomplètes pour la résolution de CSP

Résumé

L’hybridation des mécanismes de méthodes incomplètes et des techniques de programmation par contraintes est souvent basée sur des combinaisons de type maître-esclave, dédiées à la résolution de classes de problèmes spécifiques. Dans cette thèse, nous nous intéressons à la définition d’un modèle théorique uniforme, basé sur les itérations chaotiques de K.R. Apt qui définissent un cadre mathématique pour l’itération d’un ensemble fini de fonctions sur des domaines abstraits munis d’un ordre partiel. Ce cadre permet de prendre en compte une hybridation entre les méthodes incomplètes et les méthodes complètes. Dans ce contexte, la résolution s’apparente à un calcul de point fixe d’un ensemble de fonctions de réductions spécifiques. Notre cadre générique permet alors d’envisager des stratégies de combinaisons et d’hybridation de manière plus fine et d’étudier leurs propriétés. Nous avons employé un cadre général approprié pour modéliser la résolution des problèmes d’optimisation et nous présentons des résultats expérimentaux qui mettent en avant les atouts de telles combinaisons en regard d’une utilisation indépendante des techniques de résolution.

Mots-clés : CSP, recherche locale, algorithmes génétiques, propagation de contraintes, résolution hybride

Hybridization of complet and incomplete methods to solve CSP

Abstract

Hybridization of incomplete and constraint programming techniques for solving Constraint Satisfaction Problems is generally restricted to some kind of master-slave combinations for specific classes of problems. In this PhD thesis, we are concerned with the design of a hybrid resolution framework based on K.R. Apt’s chaotic iterations. In this framework, basic resolution processes are abstracted by functions over an ordered structure. This allows us to consider the different resolution agents at a same level and to study more precisely various strategies for hybridization of local search, genetic algorithms and constraint propagation. Hybrid resolution can be achieved as the computation of a fixed point of some specific reduction functions. Our framework opens up new and finer possibilities for hybridization/combination strategies. Our prototype implementation gave experimental results showing the interest of the model to design such hybridizations.

Keywords: CSP, local search, genetic algorithms, constraint propagation, hybrid resolution

TONY LAMBERT

Hybridation de méthodes complètes et incomplètes pour la résolution de CSP

Thèse de doctorat

Spécialité : Informatique

École Doctorale STIM

Sommaire

Contexte de travail

Motivations et contributions

Organisation de la thèse

Part 1 Méthodes de résolution des problèmes de satisfaction de contraintes

Chapitre 1 Les problèmes de satisfaction de contraintes

1.1 Introduction

1.2 Le modèle CSP et ses principales caractéristiques

1.3 Les problèmes d’optimisation sous contraintes

1.4 Exemples de formalisation

1.4.1 Le problème du coloriage de carte

1.4.2 Le placement de reines

1.4.3 Le problème du Zèbre

1.4.4 La règle de Golomb

1.4.5 Les carrés magiques

1.4.6 SEND + MORE = MONEY

1.4.7 Le nombre de Langford

1.4.8 Le voyageur de commerce

1.5 Conclusion

Chapitre 2 Résolution des CSP par des méthodes complètes

2.1 Introduction

2.2 Generate-and-test et backtracking

2.3 Notion de consistance

2.3.1 Consistance de noeud

2.3.2 Consistance d’arc

2.3.3 Consistance hyper-arc

2.3.4 La k-consistance

2.4 Algorithmes de filtrage et propagation de contraintes

2.4.1 Les contraintes globales

2.5 Méthodes de recherche et algorithmes de résolution

2.6 Conclusion

Chapitre 3 Résolution des CSP par des méthodes incomplètes

3.1 Introduction

3.2 La recherche locale

3.2.1 Recherche par voisinage

3.2.2 Algorithmes de recherche locale

Le Recuit Simulé Simulated Annealing

Recherche Tabou

3.3 Les algorithmes génétiques

Les populations

L’évaluation

Les opérateurs génétiques

La sélection

3.4 Conclusion

Chapitre 4 Résolution hybride

4.1 Introduction

4.2 Approches Collaboratives

4.3 Approche intégrative

4.3.1 La recherche locale au secours de l’algorithme complet

Métaheuristique pour l’obtention de bornes

Affaiblissement des méthodes complètes

4.3.2 Une méthode complète au c ur du voisinage d’une recherche locale

Recherche exacte et voisinage large

Recouper les solutions

Filtrer l’espace de recherche

Utiliser le schéma d’une méthode incomplète pour une méthode complète

4.4 Conclusion

Chapitre 5 Cadre et algorithme générique pour la propagation de contrainte

5.1 Introduction

5.2 Ordre partiel

5.3 Fonctions et propriétés

5.4 Application aux CSP et domaines composés

5.5 Algorithme générique itératif

5.6 Conclusion

Part 2 Cadre théorique uniforme pour la résolution des CSP

Chapitre 6 Introduction de la recherche locale

6.1 Introduction

6.2 Échantillons et voisinage

6.2.1 Échantillonnage et Notion de solution

6.2.2 Ordre sur les échantillons

6.3 Modèle de calcul

6.4 Les solutions

6.5 Fonctions de réduction : définition et propriétés

6.5.1 Réduction de domaines

6.5.2 Découpage de domaines

Hybridation de méthodes

complètes et incomplètes pour la

résolution de CSP

Part 1

Méthodes de résolution des

problèmes de satisfaction

de contraintes

Chapitre 1

Les problèmes de satisfaction

de contraintes

1.3 Les problèmes d’optimisation
sous contraintes

1.4.1 Le problème du coloriage
de carte

Chapitre 2

Résolution des CSP par

des méthodes complètes

Chapitre 3

Résolution des CSP par

des méthodes incomplètes

Chapitre 4

Résolution hybride

Chapitre 5

Cadre et algorithme

générique pour la propagation

de contrainte

Part 2

Cadre théorique uniforme pour la

résolution des CSP

Chapitre 6

Introduction de la recherche

locale

Chapitre 7

Modèle hybride pour

les algorithmes génétiques

Chapitre 8

Une formulation hybride

des CSP